题目内容
5. 已知:如图,M为△ABC的边BC的中点,AT平分∠BAC,交BC于T,ME∥AT交CA的延长线于E.求证:BD=CE.
已知:如图,M为△ABC的边BC的中点,AT平分∠BAC,交BC于T,ME∥AT交CA的延长线于E.求证:BD=CE.
分析 根据平行线的性质,可得∠6与∠5,∠B与∠CMG,∠4与∠6的关系,根据等腰三角形的判定,可得CE与CG的关系,根据全等三角形的判定与性质,可得BD与CG的关系,再根据等量代换,可得答案.
解答 证明:如图,过点C作AB的平行线交EM的延长线于G,则∠6=∠5,∠B=∠CMG,∠4=∠6.
∵AT‖EM,
∴∠1=∠3,∠2=∠4;
又∵AT平分∠BAC,
∴∠1=∠2,
∴∠3=∠4,
∴∠3=∠6,
∴CE=CG.
在△BDM和△CGM中,
$\left\{\begin{array}{l}{∠5=∠6}\\{∠B=∠MCG}\\{BM=CM}\end{array}\right.$,
∴△EBM≌△GCM (AAS),
∴BD=CG.
∴BD=CE.
点评 本题考查了全等三角形的判定与性质,利用了平行线的性质,等腰三角形的判定,全等三角形的判定与性质,等量代换.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
4.-1-$\frac{{a}^{2}}{a-1}$+a等于( )
| A. | $\frac{1}{1-a}$ | B. | $\frac{1}{a-1}$ | C. | -$\frac{2a-1}{a-1}$ | D. | $\frac{-2{a}^{2}-1}{a-1}$ |
 如图:
如图: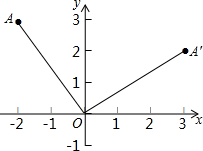 如图,点A坐标为(-2,3),将点A绕原点O顺时针旋转90°得点A′,求A′的坐标.
如图,点A坐标为(-2,3),将点A绕原点O顺时针旋转90°得点A′,求A′的坐标.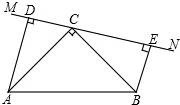 在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且
在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且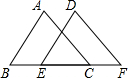 已知:如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
已知:如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.