题目内容
3. 如图,已知四边形ABCD的对角线交于点O,∠BAC=∠BDC.
如图,已知四边形ABCD的对角线交于点O,∠BAC=∠BDC.(1)求证:△ABO∽△DCO;
(2)求证:∠DAC=∠DBC.
分析 (1)由∠AOB=∠DOC,∠BAC=∠CDB,根据有两角对应相等的三角形相似,可判定△AOB∽△DOC,
(2)根据相似三角形的性质即可得OA:OB=OD:OC,又由∠AOD=∠BOC,根据两组对应边的比相等且夹角对应相等的两个三角形相似,即可判定△AOD∽△BOC,则可证得:∠DAC=∠CBD.
解答 证明:(1)∵∠AOB=∠DOC,∠BAC=∠CDB,
∴△AOB∽△DOC,
(2)∵△AOB∽△DOC,
∴OA:OD=OB:OC,
∴OA:OB=OD:OC,
∵∠AOD=∠BOC,
∴△AOD∽△BOC,
∴∠DAC=∠CBD.
点评 此题考查了相似三角形的判定与性质.熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
11.已知a2+Nab+64b2是一个完全平方式,则N等于( )
| A. | 8 | B. | ±8 | C. | ±16 | D. | ±32 |
 如图:
如图: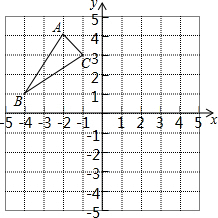 如图的方格纸中,△ABC的顶点坐标分别为A(-2,5),B(-4,1)和C (-1,3).
如图的方格纸中,△ABC的顶点坐标分别为A(-2,5),B(-4,1)和C (-1,3).