题目内容
14.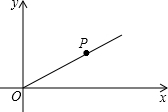 如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30°,OP=8.
如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30°,OP=8.(1)射线OP与y轴正半轴的夹角为60°.
(2)求点P的坐标.
分析 (1)根据平面直角坐标系可知OP与y轴正半轴的夹角为60°
(2)过点P作PA⊥x轴于点A,然后利用含30°的直角三角形性质求出PA与OA的长度.
解答 解:(1)根据平面直角坐标系可知OP与y轴正半轴的夹角为90°-30°=60°;
(2)过点P作PA⊥x轴于点A, ∵∠POA=30°,
∵∠POA=30°,
∴PA=$\frac{1}{2}$OP=4,
由勾股定理可知:OA=4$\sqrt{3}$
∴P的坐标为(4$\sqrt{3}$,4)
故答案为:(1)60°
点评 本题考查坐标与图形问题,解题的关键是过点P作PA⊥x轴于点A,然后利用含30°的直角三角形性质求出PA与OA的长度即可,另外注意x轴与y轴是互相垂直的.

练习册系列答案
相关题目
19.怎样测量某种食用油沸腾时的温度?因为油的沸点温度很高,用普通温度计很难直接测量,于是,小明设计了一个实验:取适量食用油在锅里用煤气灶开小火进行均匀加热,每隔5秒钟用普通温度计(测量范围在0℃-100℃之间)测量一次油温,结果如表:
而且小明发现50秒后该食用油沸腾.根据上述分析,你认为下面对该食用油沸点温度估计较为可靠的是( )
| 时间(s) | 0 | 5 | 10 | 15 |
| 食用油温度(℃) | 20 | 35 | 50 | 65 |
| A. | 85℃ | B. | 120℃ | C. | 150℃ | D. | 170℃ |
6.若|a|=$\frac{1}{5}$,|b|=5,则a÷b×$\frac{1}{b}$等于( )
| A. | $\frac{1}{125}$ | B. | ±$\frac{1}{125}$ | C. | ±$\frac{1}{5}$ | D. | -$\frac{1}{125}$或-$\frac{1}{5}$ |
3.平行四边形ABCD的四个顶点都在圆O上,那么四边形ABCD一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 以上都不对 |
 如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的角平分线FP相交于点P.若∠BEP=46°,则∠EPF=68度.
如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的角平分线FP相交于点P.若∠BEP=46°,则∠EPF=68度. 如图,长方形ABCD的面积为$\sqrt{18}$cm2,AB=$\sqrt{3}$cm,求边BC的长.
如图,长方形ABCD的面积为$\sqrt{18}$cm2,AB=$\sqrt{3}$cm,求边BC的长.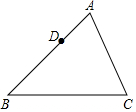 如图,已知锐角△ABC,点D是AB边上的一定点,请用尺规在AC边上求作一点E,使△ADE与△ABC相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.)
如图,已知锐角△ABC,点D是AB边上的一定点,请用尺规在AC边上求作一点E,使△ADE与△ABC相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.)