题目内容
14. 如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的角平分线FP相交于点P.若∠BEP=46°,则∠EPF=68度.
如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的角平分线FP相交于点P.若∠BEP=46°,则∠EPF=68度.
分析 由AB∥CD,根据两直线平行,同旁内角互补,即可得∠BEF+∠DFE=180°,又由EP⊥EF,∠EFD的平分线与EP相交于点P,∠BEP=36°,即可求得∠PFE的度数,然后根据三角形的内角和定理,即可求得∠EPF的度数.
解答 解:∵AB∥CD,
∴∠BEF+∠DFE=180°,
∴EP⊥EF,
∴∠PEF=90°,
∵∠BEP=36°,
∴∠EFD=180°-90°-46°=44°,
∵∠EFD的平分线与EP相交于点P,
∴∠EFP=∠PFD=$\frac{1}{2}$∠EFD=22°,
∴∠EPF=90°-∠EFP=68°.
故答案为:68.
点评 此题考查了平行线的性质与角平分线的定义,以及三角形内角和定理.此题难度不大,解题的关键是注意两直线平行,同旁内角互补定理的应用,注意数形结合思想的应用.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.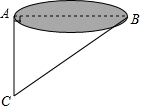 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.| A. | 75•sin55° | B. | 75•cos55° | C. | 75•tan55° | D. | $\frac{75}{tan55°}$ |
 数学问题:
数学问题: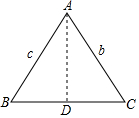 利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)
利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC) (尺规作图)已知线段a,b(a<b),求作线段AB,使AB=a+b(只需画图,不要求写画法)
(尺规作图)已知线段a,b(a<b),求作线段AB,使AB=a+b(只需画图,不要求写画法) 如图所示的正方体的棱长为2,我们知道正方体的表面展开图共有11种,请你至少画出其中的3种,并求出它们的面积.
如图所示的正方体的棱长为2,我们知道正方体的表面展开图共有11种,请你至少画出其中的3种,并求出它们的面积.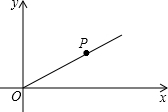 如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30°,OP=8.
如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30°,OP=8.