题目内容
3.平行四边形ABCD的四个顶点都在圆O上,那么四边形ABCD一定是( )| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 以上都不对 |
分析 首先根据$\widehat{BAD}$和$\widehat{BCD}$所对的圆心角的和是一个周角,可得∠A+∠C=180°,然后根据∠A=∠C,判断出∠A、∠C都是直角,即可推得四边形ABCD一定是矩形.
解答 解:如图,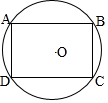 ,
,
∵$\widehat{BAD}$和$\widehat{BCD}$所对的圆心角的和是一个周角,
∴∠A+∠C=180°,
∵四边形ABCD是平行四边形,
∴∠A=∠C,
∴∠A=∠C=180°÷2=90°,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD一定是矩形.
故选:B.
点评 此题主要考查了圆内接四边形的性质和应用,以及平行四边形的性质和应用,要熟练掌握.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
18.⊙O的半径为6,弦长为一元二次方程x2-5x-6=0的两根,则弦到圆心的距离及弦所对的圆心角的度数分别是( )
| A. | $\sqrt{3}$和30° | B. | $\sqrt{3}$和60° | C. | 3$\sqrt{3}$和30° | D. | 3$\sqrt{3}$和60° |
8.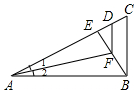 如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )
如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )
 如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )
如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )| A. | ∠1=∠EFD | B. | BE=CE | C. | BF-DE=CD | D. | DF∥BC |
15.如果两条直线被第三条直线所截,那么一对内错角的平分线的位置关系是( )
| A. | 互相垂直 | B. | 互相平行 | C. | 相交但不垂直 | D. | 不能确定 |
13. 二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值
二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值
如下表:
(1)求这个二次函数的表达式;
(2)在右图中画出此二次函数的图象的示意图;
(3)结合图象,直接写出当y>0时,自变量x的取值范围.
 二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值
二次函数y=ax2+bx+c(a≠0)图象上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{5}{2}$ | 0 | $\frac{3}{2}$ | 2 | $\frac{3}{2}$ | 0 | -$\frac{5}{2}$ | … |
(2)在右图中画出此二次函数的图象的示意图;
(3)结合图象,直接写出当y>0时,自变量x的取值范围.
 如图所示的正方体的棱长为2,我们知道正方体的表面展开图共有11种,请你至少画出其中的3种,并求出它们的面积.
如图所示的正方体的棱长为2,我们知道正方体的表面展开图共有11种,请你至少画出其中的3种,并求出它们的面积.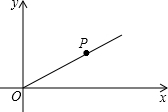 如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30°,OP=8.
如图,平面直角坐标系下,射线OP与x轴正半轴的夹角为30°,OP=8.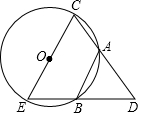 如图,CE是⊙O的直径,AB、AC是⊙O的两条弦,且AB=AC,延长CA、EB交于点D,问AD=AC吗?为什么?
如图,CE是⊙O的直径,AB、AC是⊙O的两条弦,且AB=AC,延长CA、EB交于点D,问AD=AC吗?为什么?