题目内容
20. 如图,在△ABC中,以AC为直径的⊙O分别交AB、BC于点D、E,连接DE,AD=BD,∠ADE=120°.
如图,在△ABC中,以AC为直径的⊙O分别交AB、BC于点D、E,连接DE,AD=BD,∠ADE=120°.(1)试判断△ABC的形状并说明理由.
(2)若AC=2,求图中阴影部分的面积.
分析 (1)连接CD,由AC为⊙O的直径,得到CD⊥AB,由∠ADE=120°,得到∠ACE=60°,根据等边三角形的判定即可得到结论;
(2)根据等边三角形的性质得到∠A=∠ACB=∠B=60°,推出△BDE是等边三角形,得到BD=ED,等量代换得到DE=AD,得到S阴影=S△DEB,于是得到结论.
解答 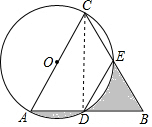 解:(1)△ABC是等边三角形,
解:(1)△ABC是等边三角形,
连接CD,
∵AC为⊙O的直径,
∴CD⊥AB,
∵AD=BD,
∴AC=BC,
∵∠ADE=120°,
∴∠ACE=60°,
∴△ABC是等边三角形;
(2)∵△ABC是等边三角形,
∴∠A=∠ACB=∠B=60°,
∴∠BED=∠BDE=∠B=60°,
∴△BDE是等边三角形,
∴BD=ED,
∵AD=BD,
∴DE=AD,
∴$\widehat{DE}$=$\widehat{AD}$,
∴S弓形DE=S弓形AD,
∴S阴影=S△DEB,
∵AC=2,
∴BD=1,
∴S阴影=S△DEB=$\frac{\sqrt{3}}{4}$.
点评 本题考查了扇形的面积,等腰三角形的性质,圆内接四边形的性质,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
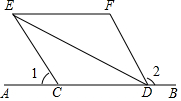 已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.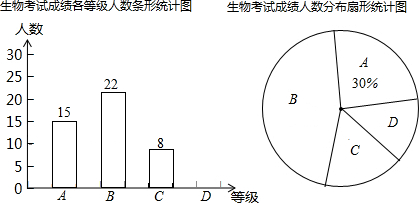
 如图,数轴上的点A所表示的分数是1$\frac{2}{5}$.
如图,数轴上的点A所表示的分数是1$\frac{2}{5}$.