题目内容
9．列方程（组）解应用题某服装店用4500元购进一批衬衫，很快售完，服装店老板又用2100元购进第二批该款式的衬衫，但每件进价比第一批衬衫的每件进价少了10元，且进货量是第一次进货量的一半，求第一批购进这种衬衫每件的进价是多少元？
分析 设第一批衬衫每件进价为x元，则第二批每件进价为（x-10）元．根据第二批该款式的衬衫，进货量是第一次的一半，列出方程即可解决问题．
解答 解：设第一批衬衫每件进价为x元，
根据题意，得$\frac{1}{2}$•$\frac{4500}{x}$=$\frac{2100}{x-10}$，
解得x=150，
经检验x=150是原方程的解，且满足题意，
答：第一批衬衫每件进价为150元．
点评 本题考查分式方程的应用，解题的关键是学会设未知数、找等量关系、列出方程解决问题，注意分式方程必须检验，属于中考常考题型．
练习册系列答案
相关题目
19．已知多项式x-a与x2+2x-1的乘积中不含x2项，则常数a的值是（ ）
| A． | -1 | B． | 1 | C． | 2 | D． | -2 |
如图，在△ABC中，以AC为直径的⊙O分别交AB、BC于点D、E，连接DE，AD=BD，∠ADE=120°．
17．
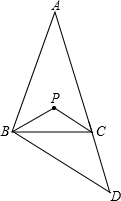如图，△ABC中，AB=AC，∠A=40°，延长AC到D，使CD=BC，点P是△ABD的内心，则∠BPC=（ ）
如图，△ABC中，AB=AC，∠A=40°，延长AC到D，使CD=BC，点P是△ABD的内心，则∠BPC=（ ）| A． | 105° | B． | 110° | C． | 130° | D． | 145° |
4．
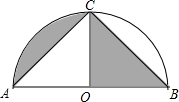如图，AB为半圆O的直径，C为$\widehat{AB}$的中点，若AB=2，则图中阴影部分的面积是（ ）
如图，AB为半圆O的直径，C为$\widehat{AB}$的中点，若AB=2，则图中阴影部分的面积是（ ）| A． | $\frac{π}{2}$ | B． | $\frac{1}{2}$+$\frac{π}{2}$ | C． | $\frac{π}{4}$ | D． | $\frac{1}{2}$+$\frac{π}{4}$ |
1．
有这样一个问题：探究函数y=$\frac{1}{（x-2）^{2}}$的图象与性质，小静根据学习函数的经验，对函数y=$\frac{1}{（x-2）^{2}}$的图象与性质进行了探究，下面是小静的探究过程，请补充完整：
（1）函数y=$\frac{1}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
表中的m=4；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；
（4）结合函数图象，写出一条该函数图象的性质：函数图象关于直线x=2对称．
有这样一个问题：探究函数y=$\frac{1}{（x-2）^{2}}$的图象与性质，小静根据学习函数的经验，对函数y=$\frac{1}{（x-2）^{2}}$的图象与性质进行了探究，下面是小静的探究过程，请补充完整：（1）函数y=$\frac{1}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
| x | … | -1 | 0 | 1 | $\frac{3}{2}$ | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{1}{9}$ | $\frac{1}{4}$ | 1 | 4 | m | 1 | $\frac{1}{4}$ | … |
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；
（4）结合函数图象，写出一条该函数图象的性质：函数图象关于直线x=2对称．