题目内容
15．
小彬所在的“数学兴趣小组”对函数y=（x-1）（x-2）（x-3）的图象与性质进行了探究，探究过程如下，请补充完整．（1）自变量x的取值范围是全体实数，x与y的几组对应值列表如下：
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
（2）在平面直角坐标系xOy中，描出了以上表中部分点的坐标，根据描出的点，画出函数y=（x-1）（x-2）（x-3）（0≤x≤4）的图象．
分析 （1）①将x=-2代入函数关系式中求出y值即可；②根据点的坐标找出函数图象关于点（2，0）对称，由此即可得出-7+n=2×2，解之即可得出结论；
（2）根据表格数据，描点、连线，画出函数图象即可．
解答 解：（1）①当x=-2时，y=（x-1）（x-2）（x-3）=-60，
∴m=-60．
故答案为：-60．
②根据表格中数据可知，函数图象关于点（2，0）对称，
∵M（-7，-720），N（n，720）为该函数图象上的两点，
∴-7+n=2×2，解得：n=11．
故答案为：11．
（2）描点、连线，画出函数图象如图所示．
点评 本题考查了二次函数的性质以及二次函数的图象，解题的关键是：（1）①代入x=-2求出y值；②根据点的坐标找出函数图象关于点（2，0）对称；（2）描点、连线，画出函数图象．
练习册系列答案
相关题目
5．已知y=3$\sqrt{x-2}+\sqrt{2-x}$+6，则x+y的立方根是（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | 8 |
6．
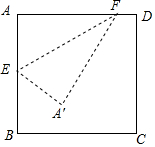如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（ ）
如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{π}{4}$ | C． | $\sqrt{2}$-1 | D． | $\frac{π}{2}$-1 |
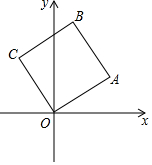已知直角坐标系中边长为1的正方形OABC，A、B，两点在第一象限．OA与x轴的角为30°，那么点B的坐标是（$\frac{\sqrt{3}-1}{2}$，$\frac{\sqrt{3}+1}{2}$）．
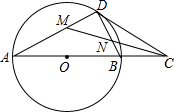如图，在⊙O中，点D是⊙O上的一点，点C是直径AB延长线上一点，连接BD，CD，且∠A=∠BDC．
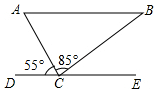如图，在△ABC中，∠ACB=85°，DE过点C，且DE∥AB，若∠ACD=55°，则∠B的度数是40°．