题目内容
15.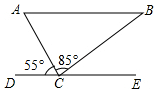 如图,在△ABC中,∠ACB=85°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是40°.
如图,在△ABC中,∠ACB=85°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是40°.
分析 由DE∥AB利用平行线的性质即可得出∠A=∠ACD,在△ABC中利用三角形内角和定理即可得出∠B=180°-∠A-∠ACB=40°,此题得解.
解答 解:∵DE∥AB,
∴∠A=∠ACD=55°,
∴∠B=180°-∠A-∠ACB=180°-55°-85°=40°.
故答案为:40°.
点评 本题考查了平行线的性质以及三角形内角和定理,熟练掌握“三角形内角和是180°”是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15. 小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.
小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
其中,①m=-60;②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(2)在平面直角坐标系xOy中,描出了以上表中部分点的坐标,根据描出的点,画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
 小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.
小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
(2)在平面直角坐标系xOy中,描出了以上表中部分点的坐标,根据描出的点,画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
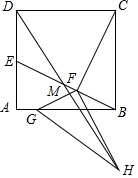 如图,正方形ABCD的边长为4,点E是AD的中点,连接BE,过点C作CF⊥BE交BE于点F,将△FBC绕F顺时针旋转得△FGH,使得点G落到线段AB上,连接DH交BE于点M,则DM的长度是$\frac{4}{11}$$\sqrt{89}$.
如图,正方形ABCD的边长为4,点E是AD的中点,连接BE,过点C作CF⊥BE交BE于点F,将△FBC绕F顺时针旋转得△FGH,使得点G落到线段AB上,连接DH交BE于点M,则DM的长度是$\frac{4}{11}$$\sqrt{89}$. 在正方形ABCD中,AB=4$\sqrt{5}$,E为BC中点,连接AE,点F为AE上一点,FE=2,FG⊥AE交DC于G,将GF绕着G点逆时针旋转使得F点正好在AD上的点H处,过点H作HN⊥HG交AB于N点,交AE于M点,则S△MNF=$\frac{96\sqrt{5}-192}{5}$.
在正方形ABCD中,AB=4$\sqrt{5}$,E为BC中点,连接AE,点F为AE上一点,FE=2,FG⊥AE交DC于G,将GF绕着G点逆时针旋转使得F点正好在AD上的点H处,过点H作HN⊥HG交AB于N点,交AE于M点,则S△MNF=$\frac{96\sqrt{5}-192}{5}$.