题目内容
6.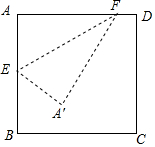 如图,在边长为1的正方形ABCD中,E、F分别为线段AB、AD、上的动点,若以EF为折线翻折,A点落在正方形ABCD所在的A′点的位置,那么A'所有可能位置形成的区域面积为( )
如图,在边长为1的正方形ABCD中,E、F分别为线段AB、AD、上的动点,若以EF为折线翻折,A点落在正方形ABCD所在的A′点的位置,那么A'所有可能位置形成的区域面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{π}{4}$ | C. | $\sqrt{2}$-1 | D. | $\frac{π}{2}$-1 |
分析 如图,以EF为折线翻折,A点落在正方形ABCD所在的A′点的位置,那么A′所有可能位置形成的图形是图中阴影部分.根据S阴=2•S扇形BAC-S正方形ABCD计算即可.
解答 解:如图,以EF为折线翻折,A点落在正方形ABCD所在的A′点的位置,那么A′所有可能位置形成的图形是图中阴影部分.
∴S阴=2•S扇形BAC-S正方形ABCD=$\frac{π}{2}$-1,
故选D.
点评 本题考查翻折变换、扇形的面积公式、正方形的性质等知识,解题的关键是正确判断等A′所有可能位置形成的图形,属于中考填空题中的压轴题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
15. 小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.
小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
其中,①m=-60;②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(2)在平面直角坐标系xOy中,描出了以上表中部分点的坐标,根据描出的点,画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
 小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.
小彬所在的“数学兴趣小组”对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
(2)在平面直角坐标系xOy中,描出了以上表中部分点的坐标,根据描出的点,画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
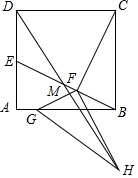 如图,正方形ABCD的边长为4,点E是AD的中点,连接BE,过点C作CF⊥BE交BE于点F,将△FBC绕F顺时针旋转得△FGH,使得点G落到线段AB上,连接DH交BE于点M,则DM的长度是$\frac{4}{11}$$\sqrt{89}$.
如图,正方形ABCD的边长为4,点E是AD的中点,连接BE,过点C作CF⊥BE交BE于点F,将△FBC绕F顺时针旋转得△FGH,使得点G落到线段AB上,连接DH交BE于点M,则DM的长度是$\frac{4}{11}$$\sqrt{89}$.