题目内容
18.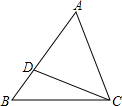 如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )(1)∠ACD=∠B;
(2)∠ADC=∠ACB;
(3)AC2=AD•AB;
(4)AB•CD=AC•BC.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由于∠DAC=∠CAB,则根据有两组角对应相等的两个三角形相似可对(1)(2)进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对(3)进行判断.
解答 解:∵∠DAC=∠CAB,
∴当∠ACD=∠B时,ACD∽△ABC;
当∠ADC=∠ACB,ACD∽△ABC;
当AD:AC=AC:AB时,即AC2=AD•AB,ACD∽△ABC.
故选C.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
8.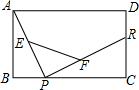 如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
 如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )| A. | 线段EF的长逐渐增大 | B. | 线段EF的长逐渐减少 | ||
| C. | 线段EF的长不变 | D. | 线段EF的长先增大后变小 |
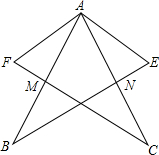 如图,AB=AC,AF=AE,AB,FC相交于点M,AC、BE相交于点N,∠FAB=∠EAC.试证明△AFM≌△AEN.
如图,AB=AC,AF=AE,AB,FC相交于点M,AC、BE相交于点N,∠FAB=∠EAC.试证明△AFM≌△AEN.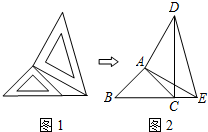 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.