题目内容
13.计算:(1)|-2|+($\frac{1}{3}$)-1×($π-\sqrt{2}$)0-$\sqrt{9}$+(-1)2
(2)(a-b+$\frac{{b}^{2}}{a+b}$)•$\frac{a+b}{a}$
(3)($\frac{3x}{x+2}$-$\frac{x}{x-2}$)÷$\frac{2x}{{x}^{2}-4}$.
分析 (1)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂、负整数指数幂法则计算,第三项利用算术平方根定义计算,最后一项利用乘方的意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,约分即可得到结果;
(3)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=2+3-3+1=3;
(2)原式=$\frac{(a+b)(a-b)+{b}^{2}}{a+b}$•$\frac{a+b}{a}$=$\frac{{a}^{2}}{a+b}$•$\frac{a+b}{a}$=a;
(3)原式=$\frac{3x(x-2)-x(x+2)}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{2x}$=3(x-2)-(x+2)=3x-6-x-2=2x-8.
点评 此题考查了分式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
1.如果把$\frac{2y}{2x-3y}$中的x和y都扩大5倍,那么分式的值( )
| A. | 扩大5倍 | B. | 不变 | C. | 缩小5倍 | D. | 扩大25倍 |
18.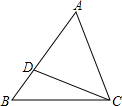 如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
(1)∠ACD=∠B;
(2)∠ADC=∠ACB;
(3)AC2=AD•AB;
(4)AB•CD=AC•BC.
 如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )(1)∠ACD=∠B;
(2)∠ADC=∠ACB;
(3)AC2=AD•AB;
(4)AB•CD=AC•BC.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.化简($\sqrt{3}$-2)2006•($\sqrt{3}$+2)2007的结果为( )
| A. | -1 | B. | $\sqrt{3}$-2 | C. | $\sqrt{3}$+2 | D. | -$\sqrt{3}$-2 |
3.若等腰三角形的两边的长是方程x2-20x+91=0的两个根,则此三角形周长为( )
| A. | 27 | B. | 33 | C. | 27和33 | D. | 21 |
 如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件:BC=EF.
如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件:BC=EF.