题目内容
6.计算:①$\frac{a}{a-b}$+$\frac{b}{b-a}$=1
②$\frac{1}{x-4}$-$\frac{8}{{x}^{2}-16}$=$\frac{1}{x+4}$.
分析 ①原式变形后,利用同分母分式的减法法则计算即可得到结果;
②原式通分并利用同分母分式的加减法则计算即可得到结果.
解答 解:①原式=$\frac{a}{a-b}$-$\frac{b}{a-b}$=$\frac{a-b}{a-b}$=1;
②原式=$\frac{x+4-8}{(x+4)(x-4)}$=$\frac{x-4}{(x+4)(x-4)}$=$\frac{1}{x+4}$,
故答案为:①1;②$\frac{1}{x+4}$
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.若二次函数y=mx2-3x+3m-m2的图象经过原点,则m的值为( )
| A. | 0或2 | B. | 3 | C. | 2 | D. | 0或$\frac{1}{2}$ |
14.下列说法中,不正确的是( )
| A. | 平方等于本身的数只有0和1 | |
| B. | 两个负数,绝对值大的负数小 | |
| C. | 正数的绝对值是它本身,负数的绝对值是它的相反数 | |
| D. | 0除以任何数都得0 |
1.如果把$\frac{2y}{2x-3y}$中的x和y都扩大5倍,那么分式的值( )
| A. | 扩大5倍 | B. | 不变 | C. | 缩小5倍 | D. | 扩大25倍 |
18.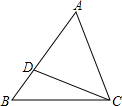 如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
(1)∠ACD=∠B;
(2)∠ADC=∠ACB;
(3)AC2=AD•AB;
(4)AB•CD=AC•BC.
 如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )(1)∠ACD=∠B;
(2)∠ADC=∠ACB;
(3)AC2=AD•AB;
(4)AB•CD=AC•BC.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.若m<n,则下列不等式中不正确的是( )
| A. | m+3<n+3 | B. | 9m<9n | C. | -m<-n | D. | $\frac{m}{2}$<$\frac{n}{2}$ |
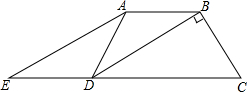 如图,在四边形ABCD中,AB=AD,BD平分∠ADC,E是CD的延长线上一点,且∠AEC=$\frac{1}{2}$∠ADC,求证:四边形ABDE是平行四边形.
如图,在四边形ABCD中,AB=AD,BD平分∠ADC,E是CD的延长线上一点,且∠AEC=$\frac{1}{2}$∠ADC,求证:四边形ABDE是平行四边形.