题目内容
3.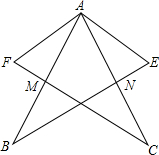 如图,AB=AC,AF=AE,AB,FC相交于点M,AC、BE相交于点N,∠FAB=∠EAC.试证明△AFM≌△AEN.
如图,AB=AC,AF=AE,AB,FC相交于点M,AC、BE相交于点N,∠FAB=∠EAC.试证明△AFM≌△AEN.
分析 可先证明△FAC与△EAB全等,得出∠F=∠E,进而可证明结论.
解答 证明:∵∠FAB=∠EAC,
∴∠FAC=∠BAE,
在△FAC和△EAB中,$\left\{\begin{array}{l}{AB=AC}\\{∠FAC=∠BAE}\\{AF=AE}\end{array}\right.$
∴△FAC≌△EAB,
∴∠F=∠E,
在△FAM和△EAN中,$\left\{\begin{array}{l}{∠F=∠E}\\{AF=AE}\\{∠FAB=∠EAC}\end{array}\right.$,
∴△AFM≌△AEN.
点评 本题考查了全等三角形的判定;熟练掌握全等三角形的判定.借助全等证明全等是经常使用的方法做题时要注意应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
14.下列说法中,不正确的是( )
| A. | 平方等于本身的数只有0和1 | |
| B. | 两个负数,绝对值大的负数小 | |
| C. | 正数的绝对值是它本身,负数的绝对值是它的相反数 | |
| D. | 0除以任何数都得0 |
18.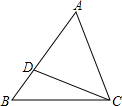 如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
(1)∠ACD=∠B;
(2)∠ADC=∠ACB;
(3)AC2=AD•AB;
(4)AB•CD=AC•BC.
 如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )
如图,点D在△ABC的边AB上,连接CD,下列条件中能判定ACD∽△ABC的共有( )(1)∠ACD=∠B;
(2)∠ADC=∠ACB;
(3)AC2=AD•AB;
(4)AB•CD=AC•BC.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.若m<n,则下列不等式中不正确的是( )
| A. | m+3<n+3 | B. | 9m<9n | C. | -m<-n | D. | $\frac{m}{2}$<$\frac{n}{2}$ |
 ∠AOC与∠BOC是一组相邻补角,OD、OE分别平分∠AOC和∠BOC,问:射线OD与射线OE的位置关系.
∠AOC与∠BOC是一组相邻补角,OD、OE分别平分∠AOC和∠BOC,问:射线OD与射线OE的位置关系.