Question

1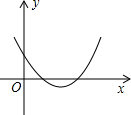．已知二次函数y=ax²+bx+c的图象如图所示，则a＞0，b＜0，c＞0，b²-4ac＞0．

Answer 1

分析 根据抛物线的开口可得出a＞0；根据抛物线与y轴交点在y轴正半轴可得出c＞0；根据抛物线对称轴为x=-$\frac{b}{2a}$=1，可得出a、b异号；根据抛物线与x轴有两个交点可得出根的判别式△＞0．结合上面结论即可解决该题．

解答 解：∵函数图象开口向上，
∴a＞0；
∵函数图象与y轴的交点在y轴正半轴上，
∴c＞0；
∵抛物线的对称轴x=-$\frac{b}{2a}$＞0，
∴a、b异号，即b＜0；
∵抛物线的图象与x轴有两个不同的交点，
∴令y=0，ax²+bx+c=0有两个不等的根，
∴△=b²-4ac＞0．
故答案为：＞；＜；＞；＞．

点评 本题考查了二次函数图象与系数的关系，解题的关键是结合函数图象分析抛物线的开口、与y轴交点、对称轴以及与x轴交点．本题属于基础题，难度不大，解决该类型题目时，结合图象逐条分析开口、对称轴、与y轴交点、与x轴交点个数（时常还会用到顶点坐标）．