题目内容
12．抛物线y=x2-（m-2）x+m+3的顶点在y轴上，则m的值为（ ）| A． | -3 | B． | 3 | C． | -2 | D． | 2 |
分析 抛物线的顶点在y轴上可得顶点的横坐标为0，即：-$\frac{-（m-2）}{2×1}$=0，就可求出m的值．
解答 解：由题可得：-$\frac{-（m-2）}{2×1}$=0，
解得m=2．
故选D．
点评 本题考查的是y轴上点的坐标特征、抛物线的顶点坐标公式，抛物线y=ax2+bx+c的顶点坐标为（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），应熟练掌握．
练习册系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
2．下列二次根式中，与$\sqrt{6}$的乘积为有理数的是（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{12}$ | C． | $\sqrt{18}$ | D． | $\sqrt{54}$ |
如图，直线a，b被直线c所截，若a∥b，∠1=110°，∠2=40°，则∠3=70°．
17．确定一个点的位置以下说法正确的是（ ）
| A． | 东北方向 | B． | 东经35°10′，北纬12° | ||
| C． | 距点A100米 | D． | 偏北20°，10000米 |
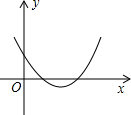已知二次函数y=ax2+bx+c的图象如图所示，则a＞0，b＜0，c＞0，b2-4ac＞0．
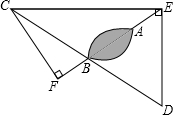海上有一小岛，为了测量小岛两端A、B的距离，测量人员设计了一种测量方法，如图所示，已知B点是CD的中点，E是BA延长线上的一点，测得AE=10海里，DE=30海里，且DE⊥EC，cos∠D=$\frac{3}{5}$．