题目内容
16．
如图，△ABC中，AC=4，BC=3，点D是点A绕着点B顺时针旋转60°得到的，则线段CD的最大值（ ）| A． | 7 | B． | 5 | C． | $\frac{7\sqrt{3}}{2}$ | D． | $\frac{5\sqrt{3}}{2}+\frac{12}{5}$ |
分析 将点A绕着点B顺时针旋转60°得到点D，即为将△ABC绕着点B顺时针旋转60°得到△BDE，根据旋转的性质得到DE=AC=4，BE=BC=3，于是得到当C，E，D共线时，CD取得最大值为7．
解答 
解：如图，将点A绕着点B顺时针旋转60°得到点D，即将△ABC绕着点B顺时针旋转60°得到△BDE，
∴DE=AC=4，BE=BC=3，
∵∠EBC=60°，
∴△BCE是等边三角形，
∴CE=BC=3，
当C，E，D共线时，CD取得最大值，
∴CD=7，
故选A．
点评 本题考查了旋转的性质，知道当C，E，D共线时，CD取得最大值是解题的关键．
练习册系列答案
相关题目
11．下列各式中一定是二次根式的是（ ）
| A． | $\sqrt{{x}^{2}+1}$ | B． | $\sqrt{x}$ | C． | $\root{3}{27}$ | D． | $\sqrt{{x}^{2}-2}$ |
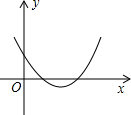已知二次函数y=ax2+bx+c的图象如图所示，则a＞0，b＜0，c＞0，b2-4ac＞0．
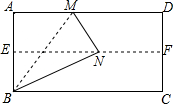如果是我们身旁没有量角器或三角尺，又需要作60°，30°，15°等大小的角，可以采用下面的方法（如图）：