题目内容
11.已知点P(a,0)和Q(b,0)是抛物线y=x2+x-6上的两个不同点,则a+b=-1.分析 由于P、Q两点的纵坐标为0,故这两点是抛物线上关于对称轴对称的两点;而抛物线y=x2+x-6的对称轴为x=-$\frac{1}{2}$,根据对称轴x=$\frac{a+b}{2}$,可求a+b的值.
解答 解:已知点P(a,0)和Q(b,0)是抛物线y=x2+x-6上的两个不同点,
因为点P(a,0)和Q(b,0)关于其对称轴对称,
而抛物线y=x2+x-6的对称轴为x=-$\frac{1}{2}$;
故有$\frac{a+b}{2}$=-$\frac{1}{2}$,
所以,a+b=-1.
故答案为:-1.
点评 本题考查了二次函数图象上点的坐特征,根据对称点与对称轴的关系得出关系式是解题的关键.

练习册系列答案
相关题目
2.下列二次根式中,与$\sqrt{6}$的乘积为有理数的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{54}$ |
16.在Rt△ABC中,∠C=90°,若tanA=$\frac{3}{4}$,则sinB的值是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{3}$ |
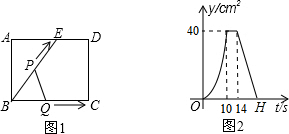
 如图,直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3=70°.
如图,直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3=70°.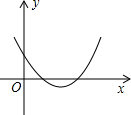 已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,b2-4ac>0.
已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,b2-4ac>0.