题目内容
18.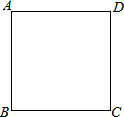 如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
如图,4个小动物分别站在正方形场地ABCD的4个顶点处,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
分析 由于速度和时间都相同,所以它们走的路程相等,可以推测:当它们同时停止时,顺次连接4个动物所在地点围成的图形是正方形,根据正方形的特征:四条边都相等,四个角都是直角,只要证明出EFGH是正方形即可.
解答  解:如图:
解:如图:
由于速度和时间都相同,所以它们走的路程相等,
AE=BF=CG=DH,
因为四边形ABCD是正方形,
所以AB=BC=CD=DA,
∠A=∠B=∠C=∠D,
因为AE=BF=CG=DH,
所以EB=FC=GD=HA,
所以△AEH≌△BFE≌△CGF≌DHG,
所以EH=EF=FG=GH,
所以四边形EFGH是菱形,
又因为△AEH≌△BFE,
所以∠AEH=BFE,
因为∠BEF+∠BFE=90°,
所以∠AEH+∠BFE=90°,
所以∠HEF=90°,
所以菱形EFGH是正方形.
点评 此题考查了正方形的特征及性质,先证明出四边形EFGH是菱形,然后根据一个角是90度的菱形是正方形即可判定.

练习册系列答案
相关题目
3.某学校为选拔数学能力突出的学生参加中学生数学竞赛,组织了多次测试,其中甲乙两位同学成绩较为优秀,他们在六次赛前测试中的成绩(单位:分)如下表所示.
如果根据这六次成绩选拔其中一人参加比赛,你认为哪一位比较合适?为什么?
| 甲 | 80 | 75 | 90 | 64 | 88 | 95 |
| 乙 | 84 | 80 | 88 | 76 | 79 | 85 |
10.某公司在A、B两地分别有库存机器16台和12台,现要运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从A地运一台到甲、乙两地的费用分别是500元和400元;从B地运一台到甲、乙两地的费用分别是300元和600元;
(1)设A地运往甲地x台挖掘机,请补全如表,并求出运这批挖掘机的总费用是多少元?
(2)当从A地运往甲地3台挖掘机时,运这批挖掘机的总费用是多少?
| 甲 | 乙 | 总计 | |
| A | x台 | (16-x)台 | 16台 |
| B | (15-x)台 | (x-3台 | 12台 |
| 总计 | 15台 | 13台 | 28台 |
(2)当从A地运往甲地3台挖掘机时,运这批挖掘机的总费用是多少?
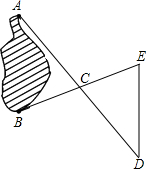 如图,A、B两点分别位于一个池塘的两端.小明想用绳子测量A、B间的距离,但绳子不够长,小明想出了这样一个办法:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A、B间的距离.请你说明其中的道理.
如图,A、B两点分别位于一个池塘的两端.小明想用绳子测量A、B间的距离,但绳子不够长,小明想出了这样一个办法:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A、B间的距离.请你说明其中的道理.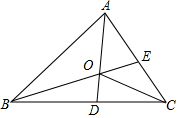 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断: