题目内容
19.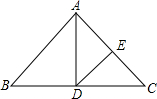 如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
分析 首先利用三角形的内角和求得∠BAC,进一步求得∠BAD,利用DE∥AB求得∠ADE=∠BAD得出答案即可.
解答 解:∵在△ABC中,∠B+∠C=100°,
∴∠BAC=80°,
∵AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=40°,
∵DE∥AB,
∴∠ADE=∠BAD=40°.
故选:B.
点评 此题考查三角形的内角和定理,角平分线的意义,平行线的性质,利用已知条件,掌握解答的步骤与方法是解决问题的关键.

练习册系列答案
相关题目
11.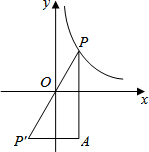 设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
 设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )
设P是函数$y=\frac{2}{x}$在第一象限的图象上的任意一点,点P关于原点的对称点为P′,过P作PA平行于y轴,过P′作P′A平行于x轴,PA与P′A交于A点,则△PAP′的面积( )| A. | 随P点的变化而变化 | B. | 等于1 | ||
| C. | 等于2 | D. | 等于4 |
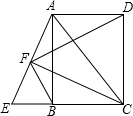 如图,E为矩形ABCD边CB延长线上一点,CE=CA,F为AE的中点,
如图,E为矩形ABCD边CB延长线上一点,CE=CA,F为AE的中点,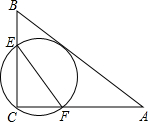 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是2.4.
如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是2.4.