题目内容
4.我们规定[a]表示实数a的整数部分,如[2.35]=2;[π]=3,按此规定[2020-$\sqrt{17}$]=2015.分析 先求出$\sqrt{17}$的范围,再求出2020-$\sqrt{17}$的范围,即可得出答案.
解答 解:∵4<$\sqrt{17}$<5,
∴-4$>-\sqrt{17}$>-5,
∴2016>2020-$\sqrt{17}$>2015,
∴[2020-$\sqrt{17}$]=2015,
故答案为:2015.
点评 本题考查了估算无理数的大小的应用,解此题的关键是求出2016>2020-$\sqrt{17}$>2015,难度不是很大.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.方程:$\frac{2}{x}$+$\frac{3}{{x}^{2}}$=1的解是( )
| A. | x=-1 | B. | x=3 | C. | x=-1或x=3 | D. | x=1或x=-312 |
19.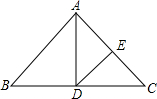 如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
 如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
9.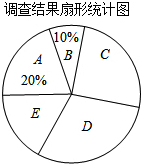 2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表.
2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)安庆市人口现有6200万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
 2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表.
2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表. | 组别 | 焦点话题 | 频数(人数) |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)安庆市人口现有6200万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
13.下列事件中,为必然事件的是( )
| A. | 购买一张彩票,中奖 | |
| B. | 一个袋中只装有2个黑球,从中摸出一个球是黑球 | |
| C. | 抛掷一枚硬币,正面向上 | |
| D. | 打开电视,正在播放广告 |
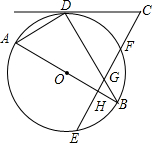 如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.
如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.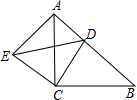 如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.  如图是某班对40名学生上学出行方式调查的扇形统计图,问:
如图是某班对40名学生上学出行方式调查的扇形统计图,问: