题目内容
10.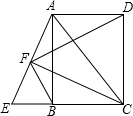 如图,E为矩形ABCD边CB延长线上一点,CE=CA,F为AE的中点,
如图,E为矩形ABCD边CB延长线上一点,CE=CA,F为AE的中点,(1)求证:BF⊥FD;
(2)若AB=8,AD=6,求DF的长.
分析 (1)由CE=CA,F为AE的中点,利用等腰三角形“三线合一”,得∠CFA=90°,再根据直角三角形斜边上的中线等于斜边的一半可得BF=EF=AF,然后利用等边对等角的性质得到∠FBA=∠FAB,从而推出∠FAD=∠FBC,再根据矩形的对边相等可得AD=BC,然后利用“边角边”即可证明△AFD≌△FBC;利用全等三角形的性质得∠BFC=∠AFD,等量代换得出结论.
(2)求出AC和BD,得出CE长,求出BE,根据勾股定理求出AE,求出BF,在△BFD中,由勾股定理求出DF即可.
解答 (1)证明:∴CE=CA,F为AE的中点,
∴∠CFE=∠AFC=90°,
∵矩形ABCD,F为AE的中点,
∴BF=EF=AF,
∴∠FBA=∠FAB,
∴∠FAD=∠FBC,
∵AD=BC,
在△AFD和△FBC中,$\left\{\begin{array}{l}{AF=BF}\\{∠FAD=∠FBC}\\{AD=BC}\end{array}\right.$,
∴△AFD≌△FBC(SAS),
∴∠BFC=∠AFD,
∴∠BFD=90°,
∴BF⊥FD;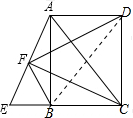
(2))解:连接BD,
∵∠ABC=90°,AB=8,AD=6,由勾股定理得:BD=AC=10=CE,
∴BE=10-6=4,
在Rt△ABE中,由勾股定理得:AE=$\sqrt{{8}^{2}{+4}^{2}}$=4$\sqrt{5}$,
∵F为AE中点,
∴BF=$\frac{1}{2}$AE=2$\sqrt{5}$,
在Rt△DFB中,DF=$\sqrt{{BD}^{2}{-FB}^{2}}$=$\sqrt{{10}^{2}{-(2\sqrt{5})}^{2}}$=4$\sqrt{5}$.
点评 本题考查了矩形性质,直角三角形斜边上中线性质,勾股定理等知识点的运用,灵活运用直角三角形斜边上中线的性质是解此题的关键,

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案 如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )
如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )| A. | 9 | B. | 8 | C. | 6 | D. | 4 |
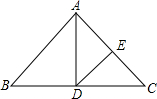 如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
| 成绩 | 频数 | 百分比 |
| 不及格 | a | m |
| 及格 | 14 | 20% |
| 良好 | b | 40% |
| 优秀 | 21 | 30% |
| 合计 | 70 | 100% |
(2)从上表的“频数”,“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校七年级体育测试成绩不及格的人数.
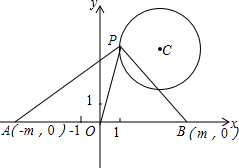 在平面直角坐标系xOy中,A(-m,0),B(m,0)(其中m>0),点P在以点C(3,4)为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,
在平面直角坐标系xOy中,A(-m,0),B(m,0)(其中m>0),点P在以点C(3,4)为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,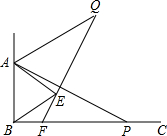 如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.
如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.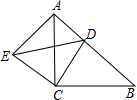 如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.