题目内容
7.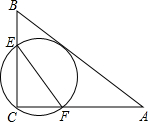 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是2.4.
如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是2.4.
分析 利用勾股定理的逆定理,由三角形的三边长可得△ABC为Rt△,根据90°的圆周角所对的弦为直径得出EF为圆的直径,又圆与AB相切,设切点为D,可知当CD⊥AB时,根据点到直线的垂线段最短可得CD最短,此时EF亦最小,由三角形ABC为直角三角形,根据直角三角形的三边长,利用面积法即可求出CD的长,即为EF的最小值.
解答 解:结合题意得,AB2=AC2+BC2,
∴△ABC为RT△,即∠C=90°,可知EF为圆的直径,
设圆与AB的切点为D,连接CD,
当CD⊥AB,即CD是圆的直径的时候,EF长度最小,
则EF的最小值是$\frac{3×4}{5}$=2.4.
故答案为:2.4.
点评 此题考查了圆周角定理,勾股定理的逆定理,垂线段最短以及切线的性质,解题的关键是根据题意得出EF为圆的直径,故当CD是直径时EF最小.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
2. 如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )
如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )
 如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )
如图,⊙O的直径CD过弦AB的中点E,且CE=2,DE=8,则AB的长为( )| A. | 9 | B. | 8 | C. | 6 | D. | 4 |
12.方程:$\frac{2}{x}$+$\frac{3}{{x}^{2}}$=1的解是( )
| A. | x=-1 | B. | x=3 | C. | x=-1或x=3 | D. | x=1或x=-312 |
19.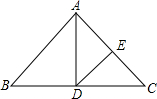 如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
 如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
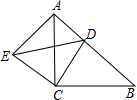 如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.