题目内容
规定△是一种新的运算符号,且a△b=a2-a×b+a-1.例如:计算2△3=22-2×3+2-1=-1.又已知|x+3|+(y-1)2=0,请你根据上面的规定试求x△y的值.
考点:有理数的混合运算,非负数的性质:绝对值,非负数的性质:偶次方
专题:新定义
分析:首先由|x+3|+(y-1)2=0得出x=-3,y=1,进一步根据规定的运算方法代入求得数值即可.
解答:解:∵|x+3|+(y-1)2=0,
∴x+3=0,y-1=0,
则x=-3,y=1,
x△y=(-3)2-(-3)×1+(-3)-1=9+3-3-1=8.
∴x+3=0,y-1=0,
则x=-3,y=1,
x△y=(-3)2-(-3)×1+(-3)-1=9+3-3-1=8.
点评:此题考查有理数的混合运算,理解规定的计算方法,列出算式是解决问题的关键.

练习册系列答案
相关题目
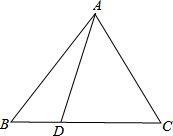 如图,在△ABC中,AB=AC,D为BC上任意一点,求证:AD2+BD•DC=AB2.
如图,在△ABC中,AB=AC,D为BC上任意一点,求证:AD2+BD•DC=AB2.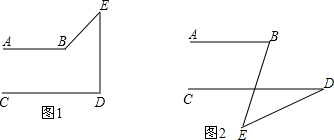 猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.
猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.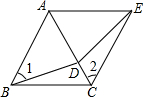 如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形.
如图所示,点D为等边△ABC的AC边上的一点,∠1=∠2,BD=CE.求证:△DAE是等边三角形. 如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.
如图,CE是△ABC的外角平分线,F是CA延长线上的一点,FG∥EC交AB于G,已知∠DCE=50°,∠ABC=40°,求∠FGA的度数.