题目内容
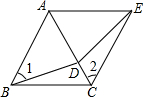如图所示，点D为等边△ABC的AC边上的一点，∠1=∠2，BD=CE．求证：△DAE是等边三角形．考点：等边三角形的判定与性质
专题：证明题
分析：由条件可证明△ABE≌△ACD，从而AE=AD，∠BAE=∠CAD=60°，所以可知△DAE是等边三角形．
解答：证明：∵三角形ABC为等边三角形
∴AB=AC
在△ABD和△ACE中
∴△ABD≌△ACE（SAS）
∴AE=AD，∠BAD=∠DAE=60°
∴△ADE是等边三角形．
∴AB=AC
在△ABD和△ACE中
|
∴△ABD≌△ACE（SAS）
∴AE=AD，∠BAD=∠DAE=60°
∴△ADE是等边三角形．
点评：本题主要考查三角形全等的判定和性质及等边三角形的判定，解题的关键是证△ABD≌△ACE．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
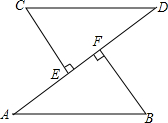如图，AB=CD，CE⊥AD于E，BF⊥AD于F，AE=DF，求证：AB∥CD．
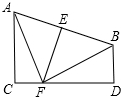已知：如图所示，AC⊥CD，BD⊥CD．线段AB的垂直平分线EF交AB于点E，交CD于点F，且AC=FD=3，CF=1求线段AB的长度．