题目内容
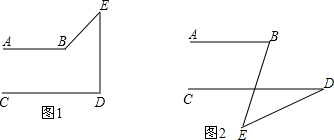 猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.
猜想:当点E在两条直线AB,CD之外时(如图1和2),∠BED,∠B,∠D满足怎样的关系时,有AB∥CD?对猜想进行证明.考点:平行线的判定
专题:
分析:(1)当∠B=∠BED+∠D时,有AB∥CD.过点E作EF∥AB.由两直线平行,同旁内角互补及已知条件∠BED=∠B+∠D求得∠FEB+∠BED+∠D=180°;然后根据平行线的传递性证得AB∥CD;
(2)当∠B=∠BED+∠D时,有AB∥CD.设BE与CD交于点O,由三角形外角的性质得出∠BOD=∠BED+∠D,则∠BOD=∠B,根据内错角相等,两直线平行即可证明AB∥CD.
(2)当∠B=∠BED+∠D时,有AB∥CD.设BE与CD交于点O,由三角形外角的性质得出∠BOD=∠BED+∠D,则∠BOD=∠B,根据内错角相等,两直线平行即可证明AB∥CD.
解答: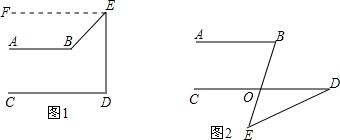 解:(1)当∠B=∠BED+∠D时,有AB∥CD.证明如下:
解:(1)当∠B=∠BED+∠D时,有AB∥CD.证明如下:
如图1,过点E作EF∥AB,则∠B+∠FEB=180°,
∵∠B=∠BED+∠D,
∴∠FEB+∠BED+∠D=180°,
∴EF∥CD,
∴AB∥CD;
(2)当∠B=∠BED+∠D时,有AB∥CD.证明如下:
如图2,设BE与CD交于点O.
∵∠BOD=∠BED+∠D,∠B=∠BED+∠D,
∴∠BOD=∠B,
∴AB∥CD.
 解:(1)当∠B=∠BED+∠D时,有AB∥CD.证明如下:
解:(1)当∠B=∠BED+∠D时,有AB∥CD.证明如下:如图1,过点E作EF∥AB,则∠B+∠FEB=180°,
∵∠B=∠BED+∠D,
∴∠FEB+∠BED+∠D=180°,
∴EF∥CD,
∴AB∥CD;
(2)当∠B=∠BED+∠D时,有AB∥CD.证明如下:
如图2,设BE与CD交于点O.
∵∠BOD=∠BED+∠D,∠B=∠BED+∠D,
∴∠BOD=∠B,
∴AB∥CD.
点评:本题考查了平行线的判定与角形外角的性质.解答此题的关键是掌握平行线的判定定理的综合运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图.
如图所示是n个小正方体搭成的几何体的俯视图,请分别画出它的主视图和左视图. 已知,如图,点B、C在线段AD上,AB=CD,EA⊥AD,BF⊥BD,CE=DF,求证:CE∥DF.
已知,如图,点B、C在线段AD上,AB=CD,EA⊥AD,BF⊥BD,CE=DF,求证:CE∥DF. 抛物线y=ax2+ax+c(a≠0)与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=3,且抛物线过点P(-1,3),求抛物线的解析式.
抛物线y=ax2+ax+c(a≠0)与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=3,且抛物线过点P(-1,3),求抛物线的解析式. 已知,如图,AC⊥BF于点C,DF⊥AB于点D,且D是AB的中点.求证:CD2=DE•DF.
已知,如图,AC⊥BF于点C,DF⊥AB于点D,且D是AB的中点.求证:CD2=DE•DF.