题目内容
如图，CE是△ABC的外角平分线，F是CA延长线上的一点，FG∥EC交AB于G，已知∠DCE=50°，∠ABC=40°，求∠FGA的度数．考点：平行线的性质,三角形的外角性质
专题：计算题
分析：根据角平分线定义得到∠3=∠1=50°，再根据平行线的性质由FG∥CE，∠F=∠3=50°，再根据三角形外角性质得∠1+∠3=∠4+∠ABC，原式可计算出∠4=60°，然后再次根据三角形外角性质由∠2=∠4-∠F进行计算即可．
解答：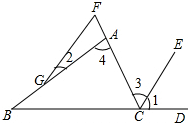
解：∵CE平分∠ACD，
∴∠3=∠1，
∴∠3=50°，
∵FG∥CE，
∴∠F=∠3=50°，
∵∠1+∠3=∠4+∠ABC，
∴∠4=50°×2-40°=60°
∴∠2=∠4-∠F=60°-50°=10°．
解：∵CE平分∠ACD，∴∠3=∠1，
∴∠3=50°，
∵FG∥CE，
∴∠F=∠3=50°，
∵∠1+∠3=∠4+∠ABC，
∴∠4=50°×2-40°=60°
∴∠2=∠4-∠F=60°-50°=10°．
点评：本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
相关题目
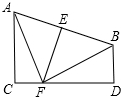已知：如图所示，AC⊥CD，BD⊥CD．线段AB的垂直平分线EF交AB于点E，交CD于点F，且AC=FD=3，CF=1求线段AB的长度．
已知，如图，AC⊥BF于点C，DF⊥AB于点D，且D是AB的中点．求证：CD2=DE•DF．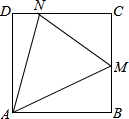
如图，正方形ABCD中，M、N分别为BC和CD边上的两点，∠MAN=45°．
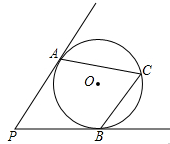如图，PA，PB分别于⊙O相切于A，B两点，∠P=70°，则∠C=