题目内容
已知一个多边形的边数增加一倍后，内角和增加1980°，求原多边形的边数．
考点：多边形内角与外角
专题：
分析：设原来的多边形的边数是n，根据多边形的内角和定理即可列方程求解．
解答：解：设原来的多边形的边数是n，依题意得．
（2n-2）•180°-（n-2）•180°=1980°，
解得：n=11．
答：原多边形的边数是11．
（2n-2）•180°-（n-2）•180°=1980°，
解得：n=11．
答：原多边形的边数是11．
点评：考查了多边形内角与外角，此题比较简单，只要结合多边形的内角和公式来寻求等量关系，构建方程即可求解．
练习册系列答案
相关题目
下列式子中，化简结果正确的是（ ）
| A、-（-5）=5 | ||||
| B、+（-5）=5 | ||||
C、|-0.5|=-
| ||||
D、+（-
|
如图所示，M是弧AB的中点，OM是⊙O 半径交弦AB于点N，AB=4
如图所示是n个小正方体搭成的几何体的俯视图，请分别画出它的主视图和左视图．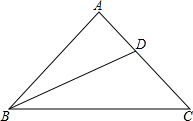
如图，在Rt△ABC中，∠A=90°，BD是角平分线，且BC=AB+AD，求证：AB=AC．
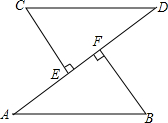如图，AB=CD，CE⊥AD于E，BF⊥AD于F，AE=DF，求证：AB∥CD．