题目内容
20. 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
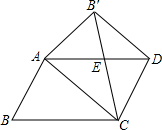
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.【发现与证明】在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.
(1)填空:B′E=DE(填“<,=,>”);
(2)求证:B′D∥AC.
【应用与探究】
在?ABCD中,已知:BC=4,∠B=60°,将△ABC沿AC翻折至△AB′C,连结B′D.若以A、C、D、B′为顶点的四边形是矩形,求AC的长.(要求画出图形)
分析 [发现与证明](1)由平行四边形的性质得出∠EAC=∠ACB,由翻折的性质得出∠ACB=∠ACB′,证出∠EAC=∠ACB′,得出AE=CE;
(2)根据等腰三角形的性质得出DE=B′E,证出∠CB′D=∠B′DA=$\frac{1}{2}$(180°-∠B′ED),由∠AEC=∠B′ED,得出∠ACB′=∠CB′D,即可得出B′D∥AC;
[应用与探究]:分两种情况:①由矩形的性质得出∠CAB′=90°,得出∠BAC=90°,再由三角函数即可求出AC;②由矩形的性质和已知条件得出AC=4$\sqrt{3}$.
解答 解:[发现与证明]:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠EAC=∠ACB,
∵△ABC≌△AB′C,
∴∠ACB=∠ACB′,BC=B′C,
∴∠EAC=∠ACB′,
∴AE=CE,
即△ACE是等腰三角形;
∴DE=B′E;
故答案为:=;
(2)∵DE=B′E,
∴∠CB′D=∠B′DA=$\frac{1}{2}$(180°-∠B′ED),
∵∠AEC=∠B′ED,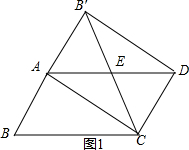
∴∠ACB′=∠CB′D,
∴B′D∥AC;
[应用与探究]:分两种情况:①如图1所示:
∵四边形ACDB′是矩形,
∴∠CAB′=90°,
∴∠BAC=90°,
∵∠B=60°,
∴AC=$\frac{\sqrt{3}}{2}$BC=2$\sqrt{3}$;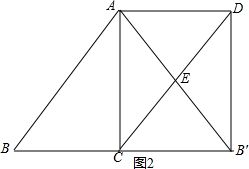
②如图2所示:
∵四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵BC=4,∠B=60°,
∴AC=4$\sqrt{3}$,
综上所述:AC的长为2$\sqrt{3}$或4$\sqrt{3}$.
点评 本题考查了平行四边形的性质、矩形的性质、翻折变换、等腰三角形的判定以及平行线的判定;熟练掌握平行四边形的性质、翻折变换的性质,并能进行推理计算是解决问题的关键.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 1 | 0.10 |
(1)频数分布表中的m=24,n=0.30;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108;
(3)根据统计数据估计该校1200名中学生中,最喜爱乒乓球这项运动的约有360人.
| A. | -$\frac{5}{4}$ | B. | -$\frac{125}{16}$ | C. | -25 | D. | 11 |
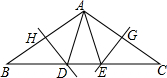 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )| A. | $\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AD,AE将∠BAC三等分 | ||
| C. | △ABE≌△ACD | D. | S△ADH=S△CEG |

 如图,已知∠B=115°,如果CD∥BE,那么∠1=65°°.
如图,已知∠B=115°,如果CD∥BE,那么∠1=65°°.