题目内容
3.如图是一个某种规律排列的数阵:
根据数阵的规律,第n行倒数第二个数是
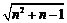 (用含n的代数式表示)
(用含n的代数式表示)
分析 探究每行最后一个数的被开方数,不难发现规律,由此即可解决问题.
解答 解:第1行的最后一个被开方数2=1×2
第2行的最后一个被开方数6=2×3
第3行的最后一个被开方数12=3×4
第4行的最后一个被开方数20=4×5,
…
第n行的最后一个被开方数n(n+1),
∴第n行的最后一数为$\sqrt{{n}^{2}+n}$,
∴第n行倒数第二个数为$\sqrt{{n}^{2}+n-1}$.
故答案为$\sqrt{{n}^{2}+n-1}$.
点评 本题考查算术平方根,解题的关键是从特殊到一般,归纳规律然后解决问题,需要耐心认真审题,属于中考常考题型.

练习册系列答案
相关题目
4.中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么-80元表示( )
| A. | 支出20元 | B. | 收入20元 | C. | 支出80元 | D. | 收入80元 |
15. 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据以上图表信息解答下列问题:
(1)频数分布表中的m=24,n=0.30;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108;
(3)根据统计数据估计该校1200名中学生中,最喜爱乒乓球这项运动的约有360人.
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 1 | 0.10 |
(1)频数分布表中的m=24,n=0.30;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108;
(3)根据统计数据估计该校1200名中学生中,最喜爱乒乓球这项运动的约有360人.

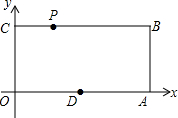 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )