题目内容
2.如果不等式组$\left\{\begin{array}{l}{\frac{x}{2}+a≥2}\\{2x-b<3}\end{array}\right.$的解集是0≤x<2,则a+b的值是3.分析 先分别解两个不等式得到x≥4-2a和x<$\frac{b+3}{2}$,再利用不等式组的解集是0≤x<1得到4-2a=0,$\frac{b+3}{2}$=2,解方程求出a和b的值,然后计算a+b.
解答 解:解不等式$\frac{x}{2}$+a≥2,得:x≥4-2a,
解不等式2x-b<3,得:x<$\frac{b+3}{2}$,
∵不等式组的解集为0≤x<2,
∴$\left\{\begin{array}{l}{4-2a=0}\\{\frac{b+3}{2}=2}\end{array}\right.$,
解得:a=2,b=1,
∴a+b=3.
故答案为:3.
点评 此题主要考查了解一元一次不等式(组),关键是正确计算出两个不等式的解集,根据不等式组的解集确定a、b的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么-80元表示( )
| A. | 支出20元 | B. | 收入20元 | C. | 支出80元 | D. | 收入80元 |
17.计算(-3)×4的结果是( )
| A. | 12 | B. | -12 | C. | -1 | D. | -7 |
7.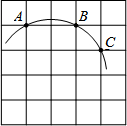 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )| A. | (0,0) | B. | (-1,1) | C. | (-1,0) | D. | (-1,-1) |





