题目内容
10.我们知道平方运算和开方运算是互逆运算,如:a2±2ab+b2=(a±b)2,那么$\sqrt{{a}^{2}±2ab+{b}^{2}}$=|a±b|,那么如何将双重二次根式$\sqrt{a±2\sqrt{b}}$(a>0,b>0,a±2$\sqrt{b}$>0)化简呢?如能找到两个数m,n(m>0,n>0),使得($\sqrt{m}$)2+($\sqrt{n}$)2=a即m+n=a,且使$\sqrt{m}$$•\sqrt{n}$=$\sqrt{b}$即m•n=b,那么a±2$\sqrt{b}$=($\sqrt{m}$)2+($\sqrt{n}$)2±2$\sqrt{m}$•$\sqrt{n}$=($\sqrt{m}$±$\sqrt{n}$)2∴$\sqrt{a±2\sqrt{b}}$=|$\sqrt{m}$±$\sqrt{n}$,双重二次根式得以化简;例如化简:$\sqrt{3+2\sqrt{2}}$;∵3=1+2 且2=1×2,∴3+2$\sqrt{2}$=($\sqrt{1}$)2+($\sqrt{2}$)2+2$\sqrt{1}$×$\sqrt{2}$∴$\sqrt{3+2\sqrt{2}}$=1+$\sqrt{2}$
由此对于任意一个二次根式只要可以将其化成$\sqrt{a±2\sqrt{b}}$的形式,且能找到m,n(m>0,n>0)使得m+n=a,且m•n=b,那么这个双重二次根式一定可以化简为一个二次根式.请同学们通过阅读上述材料,完成下列问题:
(1)填空:$\sqrt{5-2\sqrt{6}}$=$\sqrt{3}$-$\sqrt{2}$;$\sqrt{12+2\sqrt{35}}$=$\sqrt{5}$+$\sqrt{7}$;
(2)化简:①$\sqrt{9+6\sqrt{2}}$ ②$\sqrt{16-4\sqrt{15}}$
(3)计算:$\sqrt{3-\sqrt{5}}$+$\sqrt{2+\sqrt{3}}$.
分析 (1)根据二次根式的性质化简即可;
(2)先把原式化为完全平方的形式,根据二次根式的性质化简;
(3)把原式化为完全平方的形式,根据二次根式的性质化简.
解答 解:(1)$\sqrt{5-2\sqrt{6}}$=$\sqrt{({\sqrt{3})}^{2}-2×\sqrt{3}×\sqrt{2}+(\sqrt{2})^{2}}$=$\sqrt{({\sqrt{3}-\sqrt{2})}^{2}}$=$\sqrt{3}-\sqrt{2}$;
$\sqrt{12+2\sqrt{35}}$=$\sqrt{(\sqrt{7}+\sqrt{5})^{2}}$=$\sqrt{7}$+$\sqrt{5}$;
故答案为:$\sqrt{3}-\sqrt{2}$;$\sqrt{7}$+$\sqrt{5}$;
(2)①$\sqrt{9+6\sqrt{2}}$=$\sqrt{9+2\sqrt{18}}$=$\sqrt{6+2×\sqrt{6}×\sqrt{3}+3}$=$\sqrt{({\sqrt{6}+\sqrt{3})}^{2}}$=$\sqrt{6}$+$\sqrt{3}$;
②$\sqrt{16-4\sqrt{15}}$=$\sqrt{10-2\sqrt{10}×\sqrt{6}+6}$=$\sqrt{(\sqrt{10}-\sqrt{6})^{2}}$=$\sqrt{10}$-$\sqrt{6}$;
(3)$\sqrt{3-\sqrt{5}}+\sqrt{2+\sqrt{3}}$=$\sqrt{({\frac{\sqrt{10}}{2}-\frac{\sqrt{2}}{2})}^{2}}$+$\sqrt{(\frac{\sqrt{6}}{2}+\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{10}}{2}+\frac{\sqrt{6}}{2}$.
点评 本题考查的是二次根式的性质和化简,掌握二次根式的性质:$\sqrt{{a}^{2}}$=|a|和完全平方公式是解题的关键.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案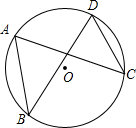 如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )
如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )| A. | 在⊙O上 | B. | 在⊙O内 | C. | 在⊙O外 | D. | 不能确定 |
| A. | b<a<c | B. | b<c<a | C. | c<b<a | D. | a<c<b |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,BD平分∠ABC,E在BC上且EF∥AB,若∠FEB=80°,则∠ABD的度数为( )
如图,BD平分∠ABC,E在BC上且EF∥AB,若∠FEB=80°,则∠ABD的度数为( )| A. | 50° | B. | 65° | C. | 30° | D. | 80° |
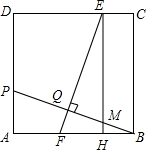 如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.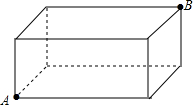 已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径.(结果保留根号)
已知长方体的长、宽、高分别为30cm、20cm、10cm,一只蚂蚁从A处出发到B处觅食,求它所走的最短路径.(结果保留根号)