题目内容
8.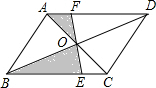 如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )
如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )| A. | 30$\sqrt{3}$ | B. | 15$\sqrt{3}$ | C. | $\frac{15}{2}$$\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 作AM⊥BC于M,由三角函数得出AM,由平行四边形的性质得出OA=OC,OB=OD,O是平行四边形的对称中心,得出△AOB的面积=$\frac{1}{4}$?ABCD的面积,四边形ABEF的面积=$\frac{1}{2}$?ABCD的面积,即可得出结果.
解答 解:作AM⊥BC于M,如图所示:
则AM=AB•sin∠ABC=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,O是平行四边形的对称中心,
∴△AOB的面积=$\frac{1}{4}$?ABCD的面积,四边形ABEF的面积=$\frac{1}{2}$?ABCD的面积,
∴图中阴影部分的面积=$\frac{1}{4}$?ABCD的面积=$\frac{1}{4}$BC•AM=$\frac{1}{4}$×10×3$\sqrt{3}$$\frac{15\sqrt{3}}{2}$;
故选C.
点评 本题考查了平行四边形的性质、三角形与四边形的面积关系;熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
相关题目
19.当前,雾霾严重.治理雾霾方法之一是将已生产的PM2.5吸纳降解.研究表明:雾霾的程度随城市中心区立体绿化面积的增大而减小,在这个问题中,自变量是( )
| A. | 城市中心立体绿化面积 | B. | PM2.5 | ||
| C. | 雾霾 | D. | 雾霾程度 |
20.函数y=$\frac{1}{{x}^{2}+ax+b}$(a,b为非0常数)取得最大值的条件是( )
| A. | a2-4b≥0 | B. | a2-4b≠0 | ||
| C. | a2-4b<0 | D. | 与a,b取值有关,不能确定 |
17.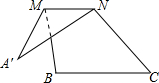 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )
 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A′=28°,∠B=120°,则∠A′NC等于( )| A. | 124° | B. | 92° | C. | 120° | D. | 116° |
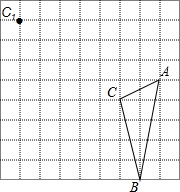 在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,
在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,