题目内容
17．
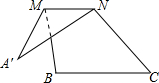如图，将△ABC沿它的中位线MN折叠后，点A落在点A′处，若∠A′=28°，∠B=120°，则∠A′NC等于（ ）| A． | 124° | B． | 92° | C． | 120° | D． | 116° |
分析 利用内角和定理求∠C，根据三角形的中位线定理可知MN∥BC，由平行线的性质可求∠A′NM、∠CNM，再利用角的和差关系求∠A′NC．
解答 解：已知∠A=∠A′=28°，∠B=120°，由三角形的内角和定理可知，
∠C=180°-∠A-∠B=32°，
∵MN是三角形的中位线，
∴MN∥BC，
∠A′NM=∠C=32°，∠CNM=180°-∠C=148°，
∴∠A′NC=∠CNM-∠A′NM=148°-32°=116°，
故选：D．
点评 本题考查图形的翻折变换的性质，翻折变换是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．
练习册系列答案
相关题目
8．
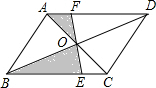如图，在?ABCD中，对角线AC与BD相交于点O，经过点O的直线之间分别交BC，AD于点E、F．若∠ABC=60°，AB=6，BC=10，则图中阴影部分的面积为（ ）
如图，在?ABCD中，对角线AC与BD相交于点O，经过点O的直线之间分别交BC，AD于点E、F．若∠ABC=60°，AB=6，BC=10，则图中阴影部分的面积为（ ）| A． | 30$\sqrt{3}$ | B． | 15$\sqrt{3}$ | C． | $\frac{15}{2}$$\sqrt{3}$ | D． | $\sqrt{3}$ |
8．
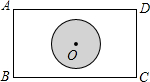如图所示，一矩形公园中有一圆形湖，湖心O恰在矩形的中心位置，若测得AB=600m，BC=800m，则湖心O到四个顶点的距离为（ ）
如图所示，一矩形公园中有一圆形湖，湖心O恰在矩形的中心位置，若测得AB=600m，BC=800m，则湖心O到四个顶点的距离为（ ）| A． | 300m | B． | 400m | C． | 500m | D． | 600m |
5．若am=2，an=3，则am-n的值是（ ）
| A． | -1 | B． | 6 | C． | $\frac{3}{4}$ | D． | $\frac{2}{3}$ |
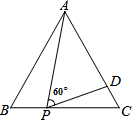如图，等边三角形△ACB的边长为3，点P为BC上的一点，点D为AC上的一点，
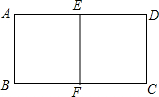用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃，设AB边长为xm，花圃面积为Sm2．
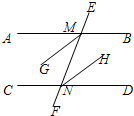如图，AB∥CD，MG平分∠AMN，NH平分∠MND．