题目内容
3.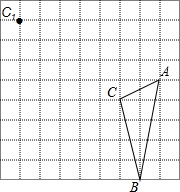 在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,
在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,(1)画出平移后的三角形△A1B1C1;
(2)求△A1B1C1的面积S;
(3)∠AA1C1+∠A1C1B1+∠C1B1B=360°.
分析 (1)首先确定A、B平移后的位置,再连接即可;
(2)把△A1B1C1放在矩形内,再利用矩形的面积减去周围多余三角形的面积即可;
(3)根据平移的性质可得AA1∥BB1,进而可得∠AA1B1+∠A1B1B=180°,再根据三角形内角和定理可得∠A1C1B1+∠C1A1B1+∠C1B1A1=180°,进而可得答案.
解答 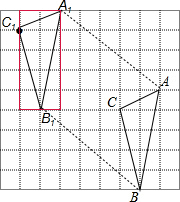 解:(1)如图所示:
解:(1)如图所示:
(2)△A1B1C1的面积:2×5-$\frac{1}{2}$×2×1-$\frac{1}{2}$×4×1-$\frac{1}{2}$×1×5=4.5;
(3)∵△ABC平移后得△A1B1C1,
∴AA1∥BB1,
∴∠AA1B1+∠A1B1B=180°,
∵∠A1C1B1+∠C1A1B1+∠C1B1A1=180°,
∴∠AA1C1+∠A1C1B1+∠C1B1B=360°,
故答案为:360°.
点评 此题主要考查了作图--平移变换,以及平行线的性质和三角形内角和,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.下列问题中,两个变量成正比例关系的是( )
| A. | 等腰三角形的面积一定,它的底边和底边上的高 | |
| B. | 等边三角形的面积与它的边长 | |
| C. | 长方形的长确定,它的周长与宽 | |
| D. | 长方形的长确定,它的面积与宽 |
8.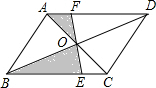 如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )
如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )
 如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )
如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )| A. | 30$\sqrt{3}$ | B. | 15$\sqrt{3}$ | C. | $\frac{15}{2}$$\sqrt{3}$ | D. | $\sqrt{3}$ |
15.已知直角三角形的一个锐角为60°,斜边长为1,那么此直角三角形的面积是( )
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |