题目内容
19．当前，雾霾严重．治理雾霾方法之一是将已生产的PM2.5吸纳降解．研究表明：雾霾的程度随城市中心区立体绿化面积的增大而减小，在这个问题中，自变量是（ ）| A． | 城市中心立体绿化面积 | B． | PM2.5 | ||
| C． | 雾霾 | D． | 雾霾程度 |
分析 根据题意确定函数与自变量的关系即可．
解答 解；雾霾的程度随城市中心区立体绿化面积的增大而减小，
雾霾的程度是城市中心区立体绿化面积的函数，城市中心区立体绿化面积是自变量，
故选：A．
点评 本题考查了常量与变量，理解常量与变量的概念、根据题意找出函数与自变量的关系是解题关键．
练习册系列答案
相关题目
9．下列运算正确的是（ ）
| A． | a2•a4=a8 | B． | 2a+3a=5a | C． | （x-2）2=x2-4 | D． | （x-2）（x+3）=x2-6 |
10．已知圆O是正n边形A1A2…An的外接圆，半径长为18，如果弧A1A2的长为π，那么边数n为（ ）
| A． | 5 | B． | 10 | C． | 36 | D． | 72 |
8．
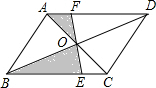如图，在?ABCD中，对角线AC与BD相交于点O，经过点O的直线之间分别交BC，AD于点E、F．若∠ABC=60°，AB=6，BC=10，则图中阴影部分的面积为（ ）
如图，在?ABCD中，对角线AC与BD相交于点O，经过点O的直线之间分别交BC，AD于点E、F．若∠ABC=60°，AB=6，BC=10，则图中阴影部分的面积为（ ）| A． | 30$\sqrt{3}$ | B． | 15$\sqrt{3}$ | C． | $\frac{15}{2}$$\sqrt{3}$ | D． | $\sqrt{3}$ |
8．
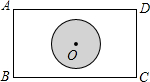如图所示，一矩形公园中有一圆形湖，湖心O恰在矩形的中心位置，若测得AB=600m，BC=800m，则湖心O到四个顶点的距离为（ ）
如图所示，一矩形公园中有一圆形湖，湖心O恰在矩形的中心位置，若测得AB=600m，BC=800m，则湖心O到四个顶点的距离为（ ）| A． | 300m | B． | 400m | C． | 500m | D． | 600m |