题目内容
20.函数y=$\frac{1}{{x}^{2}+ax+b}$(a,b为非0常数)取得最大值的条件是( )| A. | a2-4b≥0 | B. | a2-4b≠0 | ||
| C. | a2-4b<0 | D. | 与a,b取值有关,不能确定 |
分析 设t=x2+ax+b,则y=$\frac{1}{t}$,因而y是t的反比例函数,要使y取到最大值,只需t取到最小正数,由于t是x的二次函数,只需运用二次函数的最值性就可解决问题.
解答 解:设t=x2+ax+b,则y=$\frac{1}{t}$.
当x=-$\frac{a}{2}$时,t取到最小值,最小值为$\frac{4b-{a}^{2}}{4}$.
当$\frac{4b-{a}^{2}}{4}$>0即a2-4b<0时,y取得最大值.
故选C.
点评 本题主要考查了反比例函数的增减性、二次函数的最值性等知识,把原复合函数转化为反比例函数和二次函数,是解决本题的关键.

练习册系列答案
相关题目
10.已知圆O是正n边形A1A2…An的外接圆,半径长为18,如果弧A1A2的长为π,那么边数n为( )
| A. | 5 | B. | 10 | C. | 36 | D. | 72 |
8.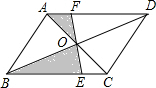 如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )
如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )
 如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )
如图,在?ABCD中,对角线AC与BD相交于点O,经过点O的直线之间分别交BC,AD于点E、F.若∠ABC=60°,AB=6,BC=10,则图中阴影部分的面积为( )| A. | 30$\sqrt{3}$ | B. | 15$\sqrt{3}$ | C. | $\frac{15}{2}$$\sqrt{3}$ | D. | $\sqrt{3}$ |
15.已知直角三角形的一个锐角为60°,斜边长为1,那么此直角三角形的面积是( )
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
8.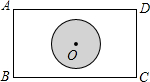 如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )
如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )
 如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )
如图所示,一矩形公园中有一圆形湖,湖心O恰在矩形的中心位置,若测得AB=600m,BC=800m,则湖心O到四个顶点的距离为( )| A. | 300m | B. | 400m | C. | 500m | D. | 600m |

 如图,△ABC中,∠ABC=40°,BD平分∠ABC,BC=BD+AD.求证:AB=AC.
如图,△ABC中,∠ABC=40°,BD平分∠ABC,BC=BD+AD.求证:AB=AC.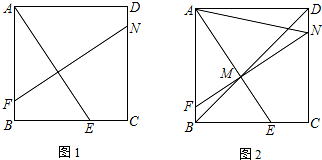
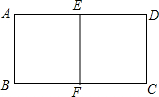 用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2.
用总长为24米的篱笆围成一个中间隔有一道篱笆的长方形花圃,设AB边长为xm,花圃面积为Sm2.