题目内容
4.如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向向内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为25cm.(1)求B点到OP的距离;
(2)求滑动支架的长.
(结果精确到0.1cm.参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
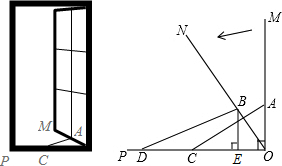
分析 (1)根据三角函数分别表示出OE和DE,再根据点D到点O的距离为25cm可列方程求解;
(2)在Rt△BDE中,根据三角函数即可得到滑动支架的长.
解答  解:(1)如图所示:在Rt△BOE中,∵∠MON=35°,
解:(1)如图所示:在Rt△BOE中,∵∠MON=35°,
∴∠BOD=55°,
∴tan55°=$\frac{BE}{OE}$,
∴OE=$\frac{BE}{{tan5{5°}}}$,
同理,DE=$\frac{BE}{{tan2{5°}}}$,
∴OD=OE+DE=$\frac{BE}{{tan5{5°}}}$+$\frac{BE}{{tan2{5°}}}$=25,
解得:BE=8.8,
答:B点到OP的距离为8.8m;
(2)在Rt△BDE中,
∵sin∠BDE=$\frac{BE}{BD}$,
∴BD=$\frac{BE}{sin∠BDE}$=$\frac{8.8}{0.42}$≈21.0(m),
答:滑动支架的长约为21.0m.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键是运用数学知识解决实际问题.

练习册系列答案
相关题目
14.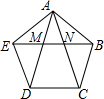 如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )
如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )
 如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )
如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )| A. | EM:AE=2:$(\sqrt{5}-1)$ | B. | MN:EM=$(\sqrt{5}-1)$:$(3-\sqrt{5})$ | C. | AM:MN=$(3-\sqrt{5})$:$(\sqrt{5}-1)$ | D. | MN:DC=$(3-\sqrt{5})$:2 |
12.若∠A是锐角,且cosA=sinA,则∠A的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 不能确定 |
9.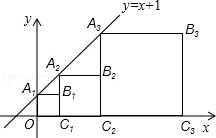 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
13.下列从左到右的变形,是因式分解的是( )
| A. | (3-x)(3+x)=9-x2 | B. | (y+1)(y-3)=(3-y)(y+1) | ||
| C. | 4yz-2y2z+z=2y(2z-zy)+z | D. | -8x2+8x-2=-2(2x-1)2 |
14.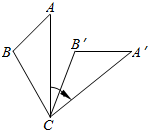 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=45°,∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=45°,∠B′=110°,则∠BCA′的度数是( )
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=45°,∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=45°,∠B′=110°,则∠BCA′的度数是( )| A. | 55° | B. | 75° | C. | 95° | D. | 110° |
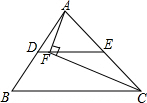 如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,且DF=1,连接AF,CF,若∠AFC=90°,则BC的长度为( )
如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,且DF=1,连接AF,CF,若∠AFC=90°,则BC的长度为( )