题目内容
9.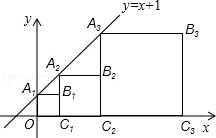 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
分析 根据直线解析式先求出OA1=1,得出B1 的纵坐标是1,再求出B2的纵坐标是2,B3 的纵坐标是22,得出规律,即可得出结果.
解答 解:∵直线y=x+1,当x=0时,y=1,当y=0时,x=-1,
∴OA1=1,OD=1,
∴∠ODA1=45°,即B1 的纵坐标是1,
∴∠A2A1B1=45°,
∴A2B1=A1B1=1,
∴A2C1=2=21,即B2的纵坐标是2,
同理得:A3C2=4=22,即B3 的纵坐标是22,…,
∴点B2016的纵坐标是22015;
故选C
点评 本题考查了一次函数图象上点的坐标特征以及正方形的性质;通过求出B1、B2、B3 的纵坐标得出规律是解决问题的关键.

练习册系列答案
相关题目
19.某校为了增强学生体质,推动“阳光体育”运动的广泛开展,学校准备购买一批运动鞋供学生借用,学校体育部从八年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和②,请根据相关信息,解答下列问题: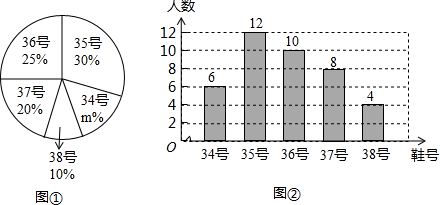
(1)图①中m的值为15;
(2)本次调查获取的样本数据的众数是35,中位数是36;
(3)该校计划购买200双运动鞋,校体育部对各种鞋号运动鞋的购买数量做出如下估计:
请你分析:校体育部的估计是否合理?如果合理,请将体育部的估算过程补充完整,若不合理,请说明理由,并且给学校提一个合理化的建议.

(1)图①中m的值为15;
(2)本次调查获取的样本数据的众数是35,中位数是36;
(3)该校计划购买200双运动鞋,校体育部对各种鞋号运动鞋的购买数量做出如下估计:
| 根据样本数据分析得知:各种鞋号的运动鞋购买数量如下: 35号:200×30%=60(只) 36号:200×25%=50(只) … |
17.学生小明、小华为了解本校八年级学生每周上网的时间,各自进行了抽样调查.小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间,算得这些学生平均每周上网时间为2.5h;小华从全体320名八年级学生名单中随机抽取了40名学生,调查了他们每周上网的时间,算得这些学生平均每周上网时间为1.2h.小明与小华整理各自样本数据,如表所示.
(每组可含最低值,不含最高值)
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?小华.
估计该校全体八年级学生平均每周上网时间为1.2h;
(2)在具有代表性的样本中,中位数所在的时间段是0~1h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?
| 时间段(h/周) | 小明抽样人数 | 小华抽样人数 |
| 0~1 | 6 | 22 |
| 1~2 | 10 | 10 |
| 2~3 | 16 | 6 |
| 3~4 | 8 | 2 |
请根据上述信息,回答下列问题:
(1)你认为哪位学生抽取的样本具有代表性?小华.
估计该校全体八年级学生平均每周上网时间为1.2h;
(2)在具有代表性的样本中,中位数所在的时间段是0~1h/周;
(3)专家建议每周上网2h以上(含2h)的同学应适当减少上网的时间,根据具有代表性的样本估计,该校全体八年级学生中有多少名学生应适当减少上网的时间?
1. 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=6,BC=4,则EC的长( )
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=6,BC=4,则EC的长( )
 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=6,BC=4,则EC的长( )
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=6,BC=4,则EC的长( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
18.一元二次方程x2-2x+m=0总有实数根,则m应满足的条件是( )
| A. | m=1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
19.在平面直角坐标系中,将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后得到点A′的坐标是( )
| A. | (0,2) | B. | (2,0) | C. | (-4,4) | D. | (3,-2) |
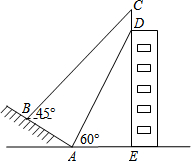 如图,一个坡度i=1:$\sqrt{3}$的小山坡,坡前高楼DE的顶端竖立一块广告牌CD,张强在山坡上点B处测量广告牌的顶端C的仰角为45°,在坡底点A处测量广告牌的底端D的仰角为60°,AB=12米,AE=18米,求这块广告牌CD的高度.(点A,B,C,D,E在同一平面内,测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,一个坡度i=1:$\sqrt{3}$的小山坡,坡前高楼DE的顶端竖立一块广告牌CD,张强在山坡上点B处测量广告牌的顶端C的仰角为45°,在坡底点A处测量广告牌的底端D的仰角为60°,AB=12米,AE=18米,求这块广告牌CD的高度.(点A,B,C,D,E在同一平面内,测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)