题目内容
13.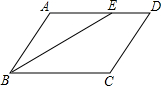 如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )
如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
分析 由平行四边形ABCD中,∠C=130°,可求得∠ABC的度数,又由BE平分∠ABC,即可求得∠CBE的度数,然后由平行线的性质,求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠ABC+∠C=180°,∠AEB=∠CBE,
∵∠C=130°,
∴∠ABC=180°-∠C=50°,
∵BE平分∠ABC,
∴∠CBE=$\frac{1}{2}$∠ABC=25°,
∴∠AEB=∠CBE=25°.
故选:D.
点评 此题考查了平行四边形的性质,属于基础题,解答本题的关键是掌握平行四边形邻角互补的性质,难度一般.

练习册系列答案
相关题目
8.已知A(x1,y1),B(x2,y2)和C(x3,y3)在直线y=-$\frac{\sqrt{3}}{2}$x+1上,若x1<x2<x3,下列判断正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
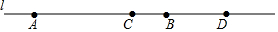 如图,直线l上有四点A、B、C、D,并且BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,如果AB、CD的中点分别为M、N,且MN=12cm,求线段AB的长.
如图,直线l上有四点A、B、C、D,并且BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,如果AB、CD的中点分别为M、N,且MN=12cm,求线段AB的长.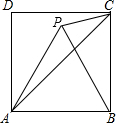 如图,四边形ABCD是边长为4的正方形,△ABP是等边三角形,则△APC的面积是4$\sqrt{3}$-4.
如图,四边形ABCD是边长为4的正方形,△ABP是等边三角形,则△APC的面积是4$\sqrt{3}$-4.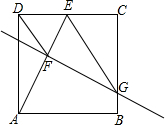 如图,在边长为4的正方形ABCD中,点E是边CD的中点,AE的垂直平分线交边BC于点G,交边AE于点F,连接DF,EG,以下结论:①DF=$\sqrt{5}$,②DF∥EG,③△EFG≌△ECG,④BG=$\frac{1}{2}$,正确的有:①④(填写序号)
如图,在边长为4的正方形ABCD中,点E是边CD的中点,AE的垂直平分线交边BC于点G,交边AE于点F,连接DF,EG,以下结论:①DF=$\sqrt{5}$,②DF∥EG,③△EFG≌△ECG,④BG=$\frac{1}{2}$,正确的有:①④(填写序号)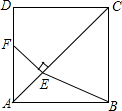 如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.