题目内容
8．已知A（x1，y1），B（x2，y2）和C（x3，y3）在直线y=-$\frac{\sqrt{3}}{2}$x+1上，若x1＜x2＜x3，下列判断正确的是（ ）| A． | y1＜y2＜y3 | B． | y1＜y3＜y2 | C． | y3＜y1＜y2 | D． | y3＜y2＜y1 |
分析 先根据一次函数的解析式判断出函数的增减性，再根据x1＜x2＜x3即可作出判断．
解答 解：∵直线y=-$\frac{\sqrt{3}}{2}$x+1中k=-$\frac{\sqrt{3}}{2}$＜0，
∴y随x的增大而减小，
∵x1＜x2＜x3，
∴y3＜y2＜y1．
故选D．
点评 本题考查的是一次函数图象上点的坐标特点，即一次函数图象上各点的坐标一定适合此函数的解析式．
练习册系列答案
相关题目
13．
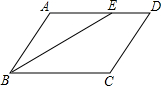如图，在?ABCD中，∠C=130°，BE平分∠ABC，则∠AEB等于（ ）
如图，在?ABCD中，∠C=130°，BE平分∠ABC，则∠AEB等于（ ）| A． | 55° | B． | 45° | C． | 35° | D． | 25° |
20．将分式$\frac{6m{n}^{3}}{4{m}^{3}n}$化成最简分式的结果正确的是（ ）
| A． | $\frac{6{n}^{2}}{4{m}^{2}}$ | B． | $\frac{6n}{4m}$ | C． | $\frac{3{n}^{2}}{2{m}^{2}}$ | D． | $\frac{3n}{2m}$ |
18．
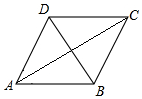如图，菱形ABCD的边长为20，∠DAB=60，对角线为AC和BD，那么菱形的面积为（ ）
如图，菱形ABCD的边长为20，∠DAB=60，对角线为AC和BD，那么菱形的面积为（ ）| A． | 50$\sqrt{3}$ | B． | 100$\sqrt{3}$ | C． | 200$\sqrt{3}$ | D． | 400$\sqrt{3}$ |