题目内容
1.计算:(1)6$\sqrt{\frac{1}{3}}$-$\sqrt{27}$+$\frac{2}{\sqrt{2}}$;
(2)($\frac{x}{y}$-$\frac{y}{x}$)÷$\frac{x-y}{x}$.
分析 (1)先把二次根式化为最简二次根式,然后化简后合并即可;
(2)先把括号内通分和除法运算化为乘法运算,然后把x2-y2分解后约分即可.
解答 解:(1)原式=2$\sqrt{3}$-3$\sqrt{3}$+$\sqrt{2}$
=-$\sqrt{3}$+$\sqrt{2}$;
(2)原式=$\frac{{x}^{2}-{y}^{2}}{xy}$•$\frac{x}{x-y}$
=$\frac{(x+y)(x-y)}{xy}$•$\frac{x}{x-y}$
=$\frac{x+y}{y}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了分式的混合运算.

练习册系列答案
相关题目
11. 如图数轴上表示的是下列哪个不等式组的解集( )
如图数轴上表示的是下列哪个不等式组的解集( )
 如图数轴上表示的是下列哪个不等式组的解集( )
如图数轴上表示的是下列哪个不等式组的解集( )| A. | $\left\{\begin{array}{l}x>-2\\ x≤3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x≥-2\\ x<3\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<-2\\ x≥3\end{array}\right.$ | D. | $\left\{\begin{array}{l}x≤-2\\ x>3\end{array}\right.$ |
13.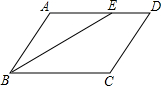 如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )
如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )
 如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )
如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
10.直线y=2x+6与x轴的交点坐标为( )
| A. | (-3,0) | B. | (3,0) | C. | (0,6) | D. | (0,-3) |
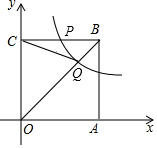 如图,平面直角坐标系中,O为坐标原点,正方形ABCO的两边OA、OC分别与x轴、y轴重合,点P是CB的中点,过点P的反比例函数y=$\frac{k}{x}$的图象交对角线OB与点Q,△COQ的面积为2,求k的值为2$\sqrt{2}$.
如图,平面直角坐标系中,O为坐标原点,正方形ABCO的两边OA、OC分别与x轴、y轴重合,点P是CB的中点,过点P的反比例函数y=$\frac{k}{x}$的图象交对角线OB与点Q,△COQ的面积为2,求k的值为2$\sqrt{2}$.