题目内容
4.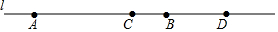 如图,直线l上有四点A、B、C、D,并且BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,如果AB、CD的中点分别为M、N,且MN=12cm,求线段AB的长.
如图,直线l上有四点A、B、C、D,并且BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,如果AB、CD的中点分别为M、N,且MN=12cm,求线段AB的长.
分析 先设CB=x,依据BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,可得AB=5x,CD=3x,再根据AB、CD的中点分别为M、N,即可得到MN=7x-$\frac{5}{2}$x-$\frac{3}{2}$x=3x,根据MN=12cm得出x的值,进而得到AB的长.
解答  解:设CB=x,则依据BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,可得AB=5x,CD=3x,
解:设CB=x,则依据BC=$\frac{1}{5}$AB=$\frac{1}{3}$CD,可得AB=5x,CD=3x,
∴AC=4x,BD=2x,AD=7x,
∵AB、CD的中点分别为M、N,
∴AM=$\frac{1}{2}$AB=$\frac{5}{2}$x,DN=$\frac{1}{2}$CD=$\frac{3}{2}$x,
∴MN=7x-$\frac{5}{2}$x-$\frac{3}{2}$x=3x,
又∵MN=12cm,
∴3x=12,
即x=4,
∴AB=5x=20,
∴AB的长度为20cm.
点评 本题主要考查了两点间的距离,解题时注意:连接两点间的线段的长度叫两点间的距离.

练习册系列答案
相关题目
14.某灯泡厂为测量一批灯泡的使用寿命,从中抽查了100只灯泡.它们的使用寿命如下表所示:
这批灯泡的平均使用寿命是( )
| 使用寿命x/小时 | 600≤x≤1000 | 1000≤x≤1400 | 1400≤x≤1800 |
| 灯泡数/个 | 30 | 30 | 40 |
| A. | 1120小时 | B. | 1240小时 | C. | 1360小时 | D. | 1480小时 |
13.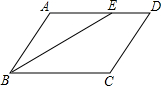 如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )
如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )
 如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )
如图,在?ABCD中,∠C=130°,BE平分∠ABC,则∠AEB等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |