题目内容
16.(1)计算:($\frac{1}{2}$)-2-6sin30°+(-2)0+|2-$\sqrt{8}$|;(2)先化简,再求值:$\frac{x-3}{x-2}$÷(x+2-$\frac{5}{x-2}$),其中x=$\sqrt{5}$-3.
分析 (1)根据负整数指数幂、锐角三角函数、零指数幂和绝对值可以解答本题;
(2)先化简式子,再将x的值代入即可解答本题.
解答 解:(1)($\frac{1}{2}$)-2-6sin30°+(-2)0+|2-$\sqrt{8}$|
=4-6×$\frac{1}{2}$+1+|2-$2\sqrt{2}$|
=4-3+1+$2\sqrt{2}$-2
=2$\sqrt{2}$;
(2)$\frac{x-3}{x-2}$÷(x+2-$\frac{5}{x-2}$)
=$\frac{x-3}{x-2}÷\frac{(x+2)(x-2)-5}{x-2}$
=$\frac{x-3}{x-2}×\frac{x-2}{{x}^{2}-9}$
=$\frac{x-3}{x-2}×\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{x+3}$,
当x=$\sqrt{5}$-3时,原式=$\frac{1}{\sqrt{5}-3+3}=\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
6.下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
| A. | x2+9=0 | B. | 4x2-4x+1=0 | C. | x2+x+1=0 | D. | x2+x-1=0 |
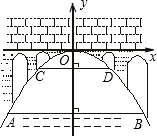 如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m.
如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升15m,水面CD的宽是10m. 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA.