题目内容
18.已知一元二次不等式ax2+bx+6>0的解集为-2<x<3,求a,b的值.分析 把已知条件转化为当-2<x<3时,抛物线y=ax2+bx+6的函数值大于0,则可确定抛物线y=ax2+bx+6与x轴的交点坐标为(-2,0),(3,0),于是可设交点式得到y=a(x+2)(x-3),然后展开后与原抛物线解析式对比可得到-6a=6,-a=b,再解方程可求出a和b的值.
解答 解:∵一元二次不等式ax2+bx+6>0的解集为-2<x<3,
∴当-2<x<3时,抛物线y=ax2+bx+6的函数值大于0,
∴抛物线y=ax2+bx+6与x轴的交点坐标为(-2,0),(3,0),
设抛物线解析式为y=a(x+2)(x-3),
即y=ax2-ax-6a,
∴-6a=6,-a=b,
∴a=-1,b=1.
点评 本题考查了一元二次不等式:一元二次不等式可通过二次函数图象进行求解.将一元二次不等式,二次函数,一元二次方程联系起来,并利用图象法进行解题,使得问题简化.

练习册系列答案
相关题目

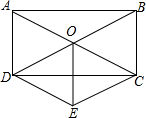 如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.
如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.