题目内容
8. 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA.(1)求证:AB+BC=2BM;
(2)求证:BC-BA=2AM.
分析 (1)延长CD交BA的延长线于点F,证△BDF≌△BDC得BC=BF,由DM⊥AB知DM∥AC,进而知AF=2AM,整理可证得结论;
(2)利用(1)中BC=BF和AF=2AM,结合线段和差可证得结论.
解答 证明:
(1)如图,延长CD交BA的延长线于点F,
∵AB=AC,∠BAC=90°,BE平分∠ABC,
∴∠FBD=∠CBD,
∵CD⊥BE,
∴∠BDF=∠BDC=90°,
在△BDF和△BDC中,
$\left\{\begin{array}{l}{∠FBD=∠CBD}\\{BD=BD}\\{∠BDF=∠BDC}\end{array}\right.$,
∴△BDF≌△BDC(ASA),
∴BF=BC,DF=DC,
∵DM⊥AB,CA⊥AB,
∴DM∥AC,
∴MF=AM,即AF=2AM
∴AB+BC=AB+AF=AB+AB+AF=2AB+2AM=2BM;
(2)由(1)可知BC=BF,
∴BC-BA=BF-BA=AF=2AM.
点评 本题主要考查全等三角形的性质与判定及三角形的中位线定理,构建全等三角形是解题关键.

练习册系列答案
相关题目
18. 用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
 用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )
用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )| A. | 22个 | B. | 19个 | C. | 16个 | D. | 13个 |
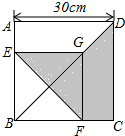 如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.
如图,ABCD和EBFG都是正方形,AB=30cm,则阴影部分的面积为450cm2.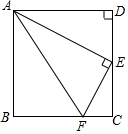 矩形ABCD,CD=6,E是CD中点,F是BC边上一点,把Rt△ABF沿AF翻折点B恰好落在E处,求AF的长.
矩形ABCD,CD=6,E是CD中点,F是BC边上一点,把Rt△ABF沿AF翻折点B恰好落在E处,求AF的长.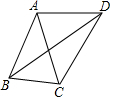 如图,AB=AC=AD,∠CBD=2∠BDC,∠BAC=40°,求∠CAD的度数.
如图,AB=AC=AD,∠CBD=2∠BDC,∠BAC=40°,求∠CAD的度数.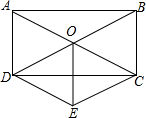 如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.
如图,矩形ABCD的两条对角线交于点O,DE∥AC,CE∥DB,DE和CE交于点E,求证:OE和CD互相垂直平分.