题目内容
1.已知实数a满足|2002-a|+$\sqrt{a-2003}$=a,则a-20022的值为2003.分析 根据二次根式有意义的条件列出不等式,求出a的范围,把原式变形,计算即可.
解答 解:由题意得,a-2003≥0,
则a≥2003,
原式变形为:a-2002+$\sqrt{a-2003}$=a,
则$\sqrt{a-2003}$=2002,
∴a=20022+2003,
则a-20022=2003.
故答案为:2003.
点评 本题考查的是二次根式有意义的条件,掌握二次根式的被开方数必须是非负数是解题的关键.

练习册系列答案
相关题目
11.有一个角为60°的菱形,边长为2,其内切圆面积为( )
| A. | $\frac{3π}{4}$ | B. | $\frac{3π}{2}$ | C. | $\frac{\sqrt{3}π}{4}$ | D. | $\frac{\sqrt{3}π}{2}$ |
12. 如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
 如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )| A. | 点B到AO的距离为sin54° | B. | 点A到OC的距离为sin36°sin54° | ||
| C. | 点B到AO的距离为tan36° | D. | 点A到OC的距离为cos36°sin54° |
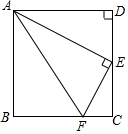 矩形ABCD,CD=6,E是CD中点,F是BC边上一点,把Rt△ABF沿AF翻折点B恰好落在E处,求AF的长.
矩形ABCD,CD=6,E是CD中点,F是BC边上一点,把Rt△ABF沿AF翻折点B恰好落在E处,求AF的长. 作出与线段AB关于y轴对称的线段A′B′.
作出与线段AB关于y轴对称的线段A′B′.