题目内容
16.我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=$\frac{p}{q}$.例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是12的最佳分解,所以F(12)=$\frac{3}{4}$.(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数.求证:对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
分析 (1)根据题意可设m=n2,由最佳分解定义可得F(m)=$\frac{n}{n}$=1;
(2)根据“吉祥数”定义知(10y+x)-(10x+y)=18,即y=x+2,结合x的范围可得2位数的“吉祥数”,求出每个“吉祥数”的F(t),比较后可得最大值.
解答 解:(1)对任意一个完全平方数m,设m=n2(n为正整数),
∵|n-n|=0,
∴n×n是m的最佳分解,
∴对任意一个完全平方数m,总有F(m)=$\frac{n}{n}$=1;
(2)设交换t的个位上的数与十位上的数得到的新数为t′,则t′=10y+x,
∵t为“吉祥数”,
∴t′-t=(10y+x)-(10x+y)=9(y-x)=18,
∴y=x+2,
∵1≤x≤y≤9,x,y为自然数,
∴“吉祥数”有:13,24,35,46,57,68,79,
∴F(13)=$\frac{1}{13}$,F(24)=$\frac{4}{6}$=$\frac{2}{3}$,F(35)=$\frac{5}{7}$,F(46)=$\frac{2}{23}$,F(57)=$\frac{3}{19}$,F(68)=$\frac{4}{17}$,F(79)=$\frac{1}{79}$,
∵$\frac{5}{7}$>$\frac{2}{3}$>$\frac{4}{17}$>$\frac{3}{19}$>$\frac{2}{23}$$>\frac{1}{13}$>$\frac{1}{79}$,
∴所有“吉祥数”中,F(t)的最大值是$\frac{5}{7}$.
点评 本题主要考查实数的运算,理解最佳分解、“吉祥数”的定义,并将其转化为实数的运算是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
5.化简:$\frac{{a}^{2}-4}{{a}^{2}+2a+1}$÷$\frac{{a}^{2}-4a+4}{(a+1)^{2}}$-$\frac{2}{a-2}$的结果为( )
| A. | $\frac{a+2}{a-2}$ | B. | $\frac{a-4}{a-2}$ | C. | $\frac{a}{a-2}$ | D. | a |
6.二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
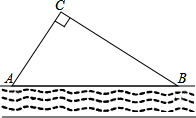 某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43) 如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.
如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是7.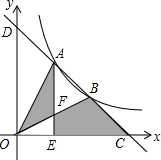 如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.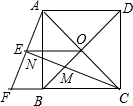 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO. 如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.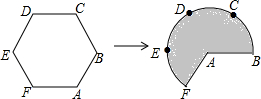 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18.
如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为18.