题目内容
6.二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )| A. | $\frac{5}{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
分析 条件m≤x≤n和mn<0可得m<0,n>0
所以y的最小值为2m为负数,最大值为2n为正数.
最大值为2n分两种情况,
(1)顶点纵坐标取到最大值,求出n=2.5,结合图象最小值只能由x=m时求出.
(2)顶点纵坐标取不到最大值,结合图象最大值只能由x=n求出,最小值只能由x=m求出.
解答 解:二次函数y=-(x-1)2+5的大致图象如下: .
.
①当m≤0≤x≤n<1时,当x=m时y取最小值,即2m=-(m-1)2+5,
解得:m=-2.
当x=n时y取最大值,即2n=-(n-1)2+5,
解得:n=2或n=-2(均不合题意,舍去);
②当m≤0≤x≤1≤n时,当x=m时y取最小值,即2m=-(m-1)2+5,
解得:m=-2.
当x=1时y取最大值,即2n=-(1-1)2+5,
解得:n=$\frac{5}{2}$,
或x=n时y取最小值,x=1时y取最大值,
2m=-(n-1)2+5,n=$\frac{5}{2}$,
∴m=$\frac{11}{8}$,
∵m<0,
∴此种情形不合题意,
所以m+n=-2+$\frac{5}{2}$=$\frac{1}{2}$.
故选:D.
点评 本题考查了二次函数的最值问题,二次函数的增减性,根据函数解析式求出对称轴解析式是解题的关键.

练习册系列答案
相关题目
17.A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了50%,而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h,则根据题意可列方程为( )
| A. | $\frac{180}{x}$-$\frac{180}{(1+50%)x}$=1 | B. | $\frac{180}{(1+50%)x}$-$\frac{180}{x}$=1 | ||
| C. | $\frac{180}{x}$-$\frac{180}{(1-50%)x}$=1 | D. | $\frac{180}{(1-50%)x}$-$\frac{180}{x}$=1 |
14.计算a10÷a2(a≠0)的结果是( )
| A. | a5 | B. | a-5 | C. | a8 | D. | a-8 |
1.计算2a2+a2,结果正确的是( )
| A. | 2a4 | B. | 2a2 | C. | 3a4 | D. | 3a2 |
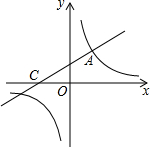 如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.