题目内容
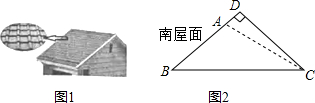
1. 如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.(1)求证:AE•BC=AD•AB;
(2)若半圆O的直径为10,sin∠BAC=$\frac{3}{5}$,求AF的长.
分析 (1)只要证明△EAD∽△ABC即可解决问题.
(2)作DM⊥AB于M,利用DM∥AE,得$\frac{DM}{AF}$=$\frac{BM}{BA}$,求出DM、BM即可解决问题.
解答 (1)证明:∵AB为半圆O的直径,
∴∠C=90°,
∵OD⊥AC,
∴∠CAB+∠AOE=90°,∠ADE=∠C=90°,
∵AE是切线,
∴OA⊥AE,
∴∠E+∠AOE=90°,
∴∠E=∠CAB,
∴△EAD∽△ABC,
∴AE:AB=AD:BC,
∴AE•BC=AD•AB.
(2)解:作DM⊥AB于M,
∵半圆O的直径为10,sin∠BAC=$\frac{3}{5}$,
∴BC=AB•sin∠BAC=6,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
∵OE⊥AC,
∴AD=$\frac{1}{2}$AC=4,OD=$\frac{1}{2}$BC=3,
∴sin∠OAD=$\frac{OD}{AO}$=$\frac{3}{5}$,
∵sin∠OAD=sin∠MAD=$\frac{DM}{AD}$,
∴DM=$\frac{12}{5}$,AM=$\sqrt{A{D}^{2}-D{M}^{2}}$=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,BM=AB-AM=$\frac{34}{5}$,
∵DM∥AE,
∴$\frac{DM}{AF}$=$\frac{BM}{BA}$,
∴AF=$\frac{60}{17}$.
点评 本题考查切线的性质、勾股定理、三角函数、平行线分线段成比例定理、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
12. 一物体的左视图和俯视图如图所示,则其主视图为( )
一物体的左视图和俯视图如图所示,则其主视图为( )
 一物体的左视图和俯视图如图所示,则其主视图为( )
一物体的左视图和俯视图如图所示,则其主视图为( )| A. |  | B. |  | C. |  | D. |  |
13.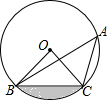 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )| A. | π-4 | B. | $\frac{2}{3}π-1$ | C. | π-2 | D. | $\frac{2π}{3}-2$ |
10.某机加工车间共有26名工人,现要加工2100个A零件,1200个B零件,已知每人每天加工A零件30个或B零件20个,问怎样分工才能确保同时完成两种零件的加工任务(每人只能加工一种零件)?设安排x人加工A零件,由题意列方程得( )
| A. | $\frac{2100}{30x}$=$\frac{1200}{20(26-x)}$ | B. | $\frac{2100}{x}$=$\frac{1200}{26-x}$ | ||
| C. | $\frac{2100}{20x}$=$\frac{1200}{30(26-x)}$ | D. | $\frac{2100}{x}$×30=$\frac{1200}{26-x}$×20 |
 如图,一个书架上的方格中放着四本厚度和长度相同的书,其中左边两边上紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,右侧书角正好靠在方格内侧上,若书架方格长BF=40cm,∠DCE=30°.
如图,一个书架上的方格中放着四本厚度和长度相同的书,其中左边两边上紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,右侧书角正好靠在方格内侧上,若书架方格长BF=40cm,∠DCE=30°.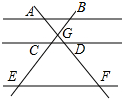 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于$\frac{3}{5}$.
如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{CE}$的值等于$\frac{3}{5}$. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论: